The previous post looked at approximations for trig functions that are simple enough to compute without a calculator. I wondered whether I could come up with something similar for logarithms. I start with log base 10. Later in the post I show how to get to find logs in other bases from logs base 10.
Let
x = m × 10p.
where 1 ≤ m ≤ 10. Then
log10(x) = log10(m) + p
and so without loss of generality we can assume 1 ≤ x ≤ 10.
But we can narrow our range a little more. If x > 3, compute the log of x‘ = x/10, and if x < 0.3 then compute the log of 10x. So we will assume
0.3 ≤ x ≤ 3.
For x in this range
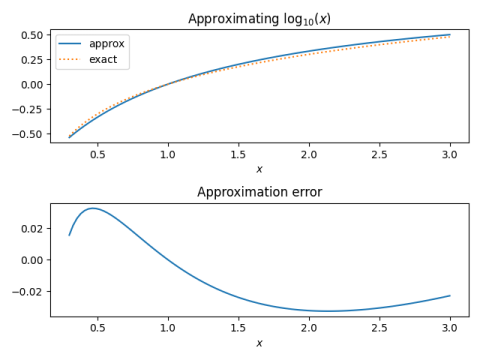
log10(x) ≈ (x − 1)/(x + 1)
is a remarkably good approximation. The absolute error is less than 0.0327 on the interval [0.3, 3].
Examples
log10 0.6 ≈ (0.6 − 1)/(0.6 + 1) = −1/4 = −0.25. Exact: −0.2218
log10 1776 = 3 + log10 1.776 ≈ 3 + 0.776/2.776 = 3.2795. Exact: 3.2494
log10 9000 = 4 + log10 0.9 ≈ 4 − 0.1/1.9 = 3.9473. Exact: 3.9542
Other bases
Logs to all bases are proportional, so you can convert between log base 10 and log to any other base by multiplying by a proportionality constant.
logb(x) = log10(x) / log10(b).
So suppose, for example, you want to compute log2 48. Since 48 = 32 × 1.5 we have
log2 48 = log2 32 + log2 1.5 = 5 + log10 1.5 / log10 2
We can approximate log10 1.5 as 1/5 and log10 2 as 1/3 to get
log2 48 = 5 + 3/5 = 5.6.
The exact value is 5.585.
If you want to use this for natural logs, you might want to memorize
1/log10 e = loge 10 = 2.3.
Update: There’s a better way to work with other bases. See this post. The same post explains why the approximation is particularly simple for logs base 10.
More accuracy
Abramowitz and Stegun refines the approximation t = (x − 1)/(x + 1). They use the interval [1/√10, √10] rather than [0.3, 3]. This slightly different interval is symmetric about 0 when you convert to t. Equation 4.1.41 runs t through a cubic polynomial and lowers the absolute error to less than 6 × 10−4. Equation 4.1.42 uses a 9th degree polynomial in t to lower the absolute error below 10−9.
Next
My next post will show how to compute 10x analogously.

Wow, nice.
There is this easy formula as well. Not as convenient for mental calculation though: https://physicsgarage.com/log-and-antilog/
You’ll be happy to know that Abramowitz and Stegun and now available online as the NIST Digital Library of Mathematical Functions. You can link directly to the page that has the equations that you reference in the “More Accuracy” section.
Rick, that’s awesome-