Computing normal probabilities with a simple calculator

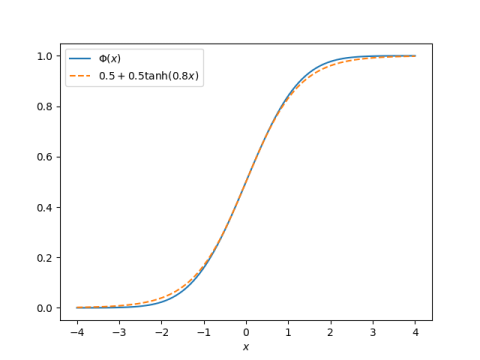
If you need to calculate Φ(x), the CDF of a standard normal random variable, but don’t have Φ on your calculator, you can use the approximation [1]

Φ(x) ≈ 0.5 + 0.5*tanh(0.8 x).

If you don’t have a tanh function on your calculator, you can use

tanh(0.8x) = (exp(1.6x) – 1) / (exp(1.6x) + 1).

This saves a few keystrokes over computing tanh directly from its definition [2].

Example

For example, suppose we want to compute Φ(0.42) using bc, the basic calculator on Unix systems. bc only comes with a few math functions, but it has a function e for exponential. Our calculation would look something like this.

    > bc -lq
    t = e(1.6*0.42); (1 + (t-1)/(t+1))/2
    .66195084790657784948

The exact value of Φ(0.42) is 0.66275….

Plots

It’s hard to see the difference between Φ(x) and the approximation above.

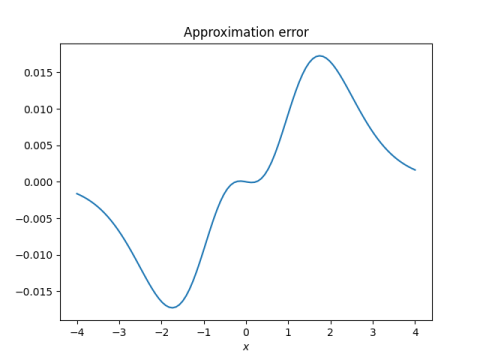
A plot of the approximation error shows that the error is greatest in [-2, -1] and [1, 2], but the error is especially small for x near 0 and x far from 0.

Related posts

• Stand-alone implementation of Φ(x)
• Integral approximation trick
• Best rational approximations for π
• Normal probability distribution approximation error

[1] Anthony C. Robin. A Quick Approximation to the Normal Integral. The Mathematical Gazette, Vol. 81, No. 490 (Mar., 1997), pp. 95-96

[2] Proof: tanh(x) is defined to be (e^x – e^–x) / (e^x + e^–x). Multiply top and bottom by e^x to get (e^2x – 1) / (e^2x + 1).