Arithmetic-geometric mean

Posted on by John

The previous post made use of both the arithmetic and geometric means. It also showed how both of these means correspond to different points along a continuum of means. This post combines those ideas.

Let a and b be two positive numbers. Then the arithmetic and geometric means are defined by

A(a, b) = (a + b)/2
G(a, b) = √(ab)

The arithmetic-geometric mean (AGM) of a and b is the limit of the sequence that takes the arithmetic and geometric mean of the arithmetic and geometric mean over and over. Specifically, the sequence starts with

a0 = A(a, b)
b0 = G(a, b)

and continues

an+1 = A(an, bn)
bn+1 = G(an, bn)

AGM(a, b) is defined as the common limit of the a‘s and the b‘s [1].

The arithmetic mean dominates the geometric mean. That is,

G(a, b) ≤ A(a, b)

with equality if and only if a = b. So the a‘s converge down to AGM(a, b) and the b‘s converge up to AGM(a, b). The AGM is between the arithmetic and geometric means.

There’s another way to create means between the arithmetic and geometric means, and that is by varying the parameter r in the family of means

\mathfrak{M}_r(x) = \left( \frac{1}{n} \sum_{i=1}^n x_i^r \right)^{1/r}

The arithmetic mean corresponds to r = 1 and the geometric mean corresponds to the limit as r approaches 0. So if r is between 1 and 0, we have a mean that’s somewhere between the arithmetic and geometric mean. For a fixed argument, these means are an increasing function of r as discussed here.

So here’s the idea I wanted to get to. Since the AGM is between the arithmetic and geometric mean, as are the r-means for r between 0 and 1, is there some value of r where the AGM is well approximated by an r-mean? This question was inspired by the result I wrote about here that the perimeter of an ellipse is very well approximated by an r-mean of its axes.

We can simplify things a little by assuming one of our arguments is 1. This is because all the means mentioned here are homogeneous, i.e. you can pull out constants.

I looked at AGM(1, x) for x ranging from 1 to 100 and compared it to r-means for varying values of r and found that I got a good fit for r = 0.415. I have no theory behind this, just tinkering. The optimal value depends on how you measure the error, and probably depends on the range of x.

When I plot AGM(1, x) and M0.415(1, x) it’s hard to tell the lines apart. Here’s what I get for their relative difference.

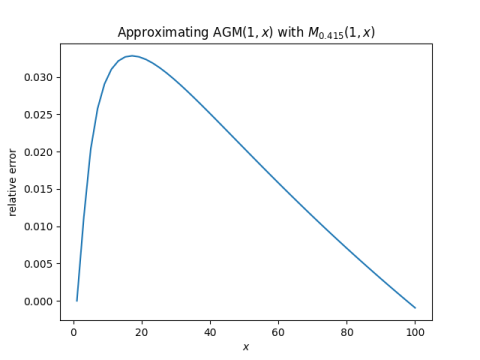
Approximating AGM$(1, x)$ with $M_{0.415}(1, x)$

There’s a connection between the AGM and elliptic functions, and so maybe r-means provide useful approximations to elliptic functions.

[1] The sequence converges very rapidly. I intended to show a plot, but the convergence is so rapid that it’s hard to plot. If I start with a = 1 and b = 100, then a and b agree to 44 significant figures after just 7 iterations.

4 thoughts on “Arithmetic-geometric mean”

  1. Very neat parameterisation. For anyone who else may be wondering, the final of the 3 classical Pythagorean means, the harmonic mean, is obtained by setting r=-1. So, the harmonic, geometric and arithmetic means correspond to r=-1, r=0 and r=1 respectively. (In the case of r=0 it’s actually defined in the limit as John mentions).

  2. lagomoof

    Despite sharing many useful properties, the AGM lacks a property that all the r-means share, which is that in general Mr(Mr(a,b),Mr(c,d)) = Mr(Mr(a,c),Mr(b,d)) for positive real a, b, c and d.

    This is a curious discrepancy considering the AGM can be ‘built’ from two r-means.

Comments are closed.