Perfect fifths, octaves, and an ergodic map

In music, a perfect fifth is the interval between two notes whose frequencies are in 3:2 ratio. For example, the interval from an A at 440 Hz and an E at 660 Hz is a perfect fifth.

Going up by 12 perfect fifths is very nearly the same as going up 7 octaves. That is,

(3/2)¹² ≈ 2⁷

or in other words,

2^7/12 ≈ 3/2.

This is why equal temperament tuning works. More on that here.

53-note scale

Going back to our first approximation, we can say that (12, 7) is an approximate solution to the equation

(3/2)^x = 2^y.

One could naturally ask whether there are better approximate solutions. One such solution, dating back to 40 BC, came from the Chinese scholar King Fang [1]. He discovered that (53, 31) is a substantially more accurate solution than (12, 7), between 6 and 7 times better.

    >>> 1.5**12/2**7
    1.0136432647705078
    >>> 1.5**53/2**31
    1.0020903140410862

In other words, going up 53 perfect fifths is nearly the same as going up 31 octaves. You could divide the octave into 53 parts using perfect fifths; we will demonstrate this visually below. However, we’re moving more the realm of number theory than practical music theory at this point.

Powers of 2 and 3

We could change our problem slightly, making it mathematically simpler though less obviously related to music, by putting all our powers of 2 on one side and looking for powers of 3 that approximately equal powers of two. That is, we could look at approximate solutions to

3^x = 2^y.

where now x and y have different meanings; our new y is our old y plus our old x. No power of 3 will ever equal a power of 2, but you can find powers of 3 close to powers of 2, making the ratio as small as you’d like.

Ergodic map

Taking the logarithm of both sides in base 2, we recast the problem as looking for integers n such that

log₂(3) n

is approximately an integer.

If we define k = log₂(3), we are looking for n such that kn mod 1, the integer part of kn, is near 0.

The map

n → kn mod 1

is ergodic because k is irrational, and so its image in the unit interval is dense as n goes to infinity. This means we can find solutions as close we’d like to 0. It also means we can find solutions as close as we’d like to any other number in the interval.

Here’s a plot of our map for n up to 12.

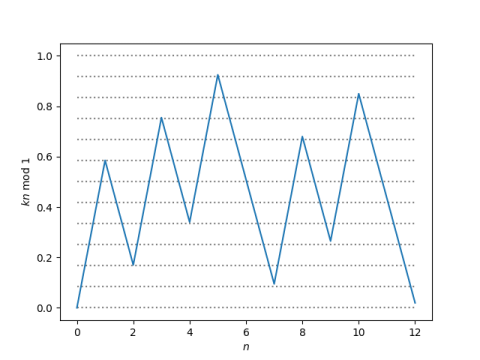
Note that the range of the map falls very nearly on the 12 evenly-spaced horizontal lines. This corresponds to the circle of fifths filling in the 12 notes of the chromatic scale.

Now let’s keep going for n up to 53.

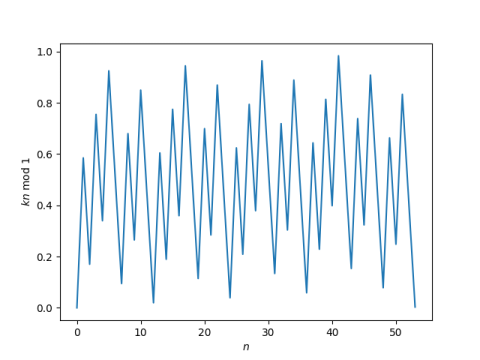
Look closely at the bottom of the plot. The graph gets close to 0 at 12, and it gets even closer to 0 at 53. The value of kn mod 1 doesn’t get smaller than the value at n = 53 until n = 359 where the value is about twice as small.

When we go up by 12 perfect fifths, we don’t end up exactly on the note we started on; 12 fifths is a little more than 7 octaves. If we keep going up in fifths we fill in notes a little higher than the original chromatic scale. Here’s a plot for n up to 24, with the values sorted so we can focus on the range rather than the ups and downs of filling in the range.

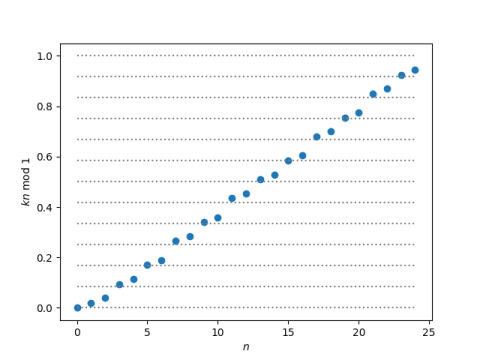
Every note in the original chromatic scale now has a counterpart that’s somewhere around 25 cents sharp.

If we keep going to n = 53, we fill in the octave more evenly. Here’s a plot of the sorted values.

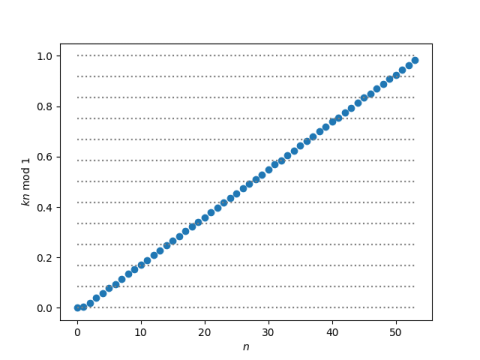
Related posts

• What key has 30 sharps?
• Listening to golden angles
• What does ergodic mean?
• The mathematics of Deep Note

[1] A. L. Leigh Silver. Some Musico-Mathematical Curiosities. The Mathematical Gazette , Feb., 1964, Vol. 48, No. 363 (Feb., 1964), pp. 1-17.