A couple days ago, near the end of a post, I mentioned exact sequences. This term does not mean what you might reasonably think it means. It doesn’t mean exact in the sense of not being approximate.
It means that the stuff that comes out of one step is exactly the stuff that gets set to 0 in the next step. That is, the image of each function is exactly the kernel of the next function in the sequence [1].
Gradient and curl
For example, let f be gradient and let g be curl. Then the following sequence is exact
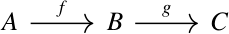
if A is the set of smooth functions from ℝ³ to ℝ, and B and C are set of smooth functions ℝ³ to ℝ³.
This says that the image of f, vector fields that are the gradient of something, is the kernel of g, vector fields with zero curl. In other lingo, gradient vector fields are irrotational, and all irrotational vector fields are the gradient of some potential function.
To show that
image f = kernel g
we have to show two things:
image f ⊂ kernel g
and
image f ⊃ kernel g
As is often the case, the former is easier than the latter. It’s a common homework problem [2] to show that the curl of a divergence is zero, i.e.
∇×(∇φ) = 0
It’s not so easy to show that for every vector field F with ∇×F = 0 there exists a potential φ such that F = ∇φ. It’s easier to show that the image of the first function part of the kernel of the next than to show that the kernel of the first is exactly the kernel of the next, because the latter requires proving the existence of something.
Short exact sequences
A short exact sequence is an exact sequence of the following form. (It’s called short because exact sequences are often longer.)
![]()
There’s no label on the arrow from 0 to A because there’s only one function from 0 to anywhere. There’s also no label on the arrow from C to 0 because there’s only one function that goes from anywhere to 0 [3].
The zero on the left implies that the function f is one-to-one (injective). It’s image is only one element, so the kernel of f is only one element.
Similarly the zero on the right end implies that the function g is onto (surjective). The kernel of the last arrow is everything in C, so the image of g has to be everything in C.
For example, let B be a group and suppose φ is a homomorphism from B to another group. Let A be the kernel of φ and let f be the inclusion map from the kernel into B. Let g be quotient map taking C = B/A. Then the so-called “first group homomorphism theorem” says that the sequence above is exact.
Div, grad, curl and all that
The title of this section is an homage to an excellent little book by H. M. Schey.
We said above that the curl of a gradient is zero, and that all vector fields with zero curl are gradients. It’s also true that the divergence of a curl is zero, and that a vector field is has zero divergence if it is the curl of something. That is, for a vector field F,
∇ · (∇ × F) = 0
and if ∇ · G = 0 for a vector field G then there exists a vector field F such that
∇×F = G.
This means we can extend our example above to
![]()
if we define A carefully.
The discussion in this section only justifies the labeled arrows. We need to justify the two unlabeled arrows on the ends.
The zero on the left requires the gradient be one-to-one. But in general, the gradient is not one-to-one: functions that differ by a constant have the same gradient. But if we define A to be the set of integrable functions on ℝ³ then the gradient is one-to-one. Requiring the integral of a function over ℝ³ to exist means the functions must eventually approach zero in every direction.
The zero on the right requires every smooth function on ℝ³ to be the divergence of something. That’s easy. Given a function φ from ℝ³ to ℝ, let F be the vector field whose first component at (x, y, z) is the integral of φ from the origin to (x, 0, 0) and whose second and third components are 0. Then the divergence of F equals φ.
Long(er) exact sequences
The exact sequence in the previous section is longer than a short exact sequence, and longer exact sequences come up in practice. An exact sequence could be infinite in one or both directions. For example, the Mayer–Vietoris sequence, a foundational tool in homology, is infinite on its left and terminates in 0 on its right end.
Related posts
- Diagram chasing: four, five, and nine lemmas
- Next areas of math to be applied
- How areas of math are connected
[1] The term “zero” is overloaded here. It could be the integer 0, or the origin of a vector space, or the kernel of a group, etc.
Everything here generalizes to objects and morphisms in a category, in which case the objects are not necessarily sets, and the morphisms are not necessarily functions. Then we don’t talk about images and kernels but about morphisms being monomorphisms and epimorphisms.
[2] There is a lot of foreshadowing in textbooks. It’s common for an author to include exercises and examples that are important later. This is often intentional, sort of an Easter egg. But sometimes the author is unconsciously pulling from experience.
[3] This observation is turned into a definition in category theory: a zero object is defined as one that is initial and final. That is, there is only one morphism from it to any other object, and only one morphism from any object to it.
