The previous post on the Yule-Simon distribution mentioned the zeta distribution at the end. This is a powerlaw distribution on the positive integers with normalizing constant given by the Riemann zeta distribution. That is, the zeta distribution has density
f(k; s) = k–s / ζ(s).
where k is a positive integer and s > 1 is a fixed parameter.
For s > 1, the zeta function is defined as the sum of the positive integers to the power negative s, so ζ(s) is essentially defined as the normalizing constant of the zeta distribution.
I wanted to make a couple comments about this. First, it shows that the zeta function appears in applications outside of number theory. Second, when working with the zeta distribution, it would be useful to have an estimate for ζ(s).
Zeta function bounds
The integral test in calculus is typically presented as a way to test whether an infinite sum converges. This is a shame. In analysis as in statistics, estimation is better than testing. Testing throws away continuous information and replaces it with a single bit.
Let f(x) be a decreasing function; we have in mind f(x) = 1/xs. Then for any n,
To estimate a sum over k, we sum the first n terms directly and apply the inequalities above for the rest. Typically n will be small, maybe 0 or 1. A larger value of n will give more accurate bounds but at the expense of a more complicated expression.
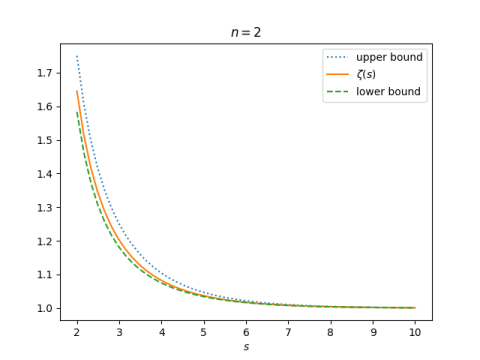
When f(x) = 1/xs and n is at least 1, we have
This says
This gives a good lower bound but a bad upper bound when we choose n = 1.
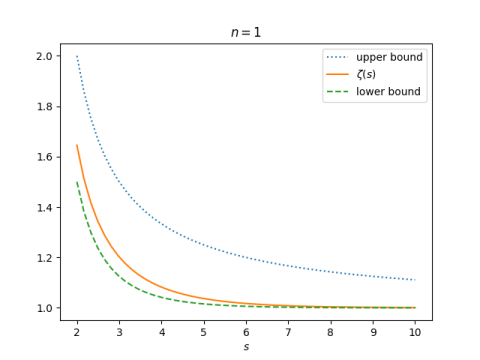
But it gives a much better upper bound when we choose n = 2.