The big idea
The Cauchy integral theorem says that the integral of a function around a closed path in the complex plane depends only on the poles of the integrand inside the path. You can change the path itself however you like as long as you don’t change which poles are inside. This observation is often used to compute real integrals using complex analysis.
Suppose you want to integrate a function f along (some portion of) the real line, and f extends to a function in the complex plane that is analytic except at poles. You may be able to evaluate your real integral using a complex contour, or more commonly, a limit of contours. You show that in some limit, the contribution to the integral along the parts of the contour you don’t need goes to zero, and the rest of the contour approaches the part you wanted to integrate over initially.
Keyhole contours
There area a handful of integration contours that come up most frequently, and the keyhole is one of them. The initial motivation for this post was the cover of the fourth edition of A Course of Modern Analysis by Whittaker and Watson. I’ve written a couple posts lately about the story behind images on book covers, and this is another post in that series.

The most recent edition has a more prosaic cover with only words and no image. However, the latest addition is much more attractive inside, having been rewritten in LaTeX.
The image on the cover is a keyhole contour. Typically the slot in the contour runs along the real axis, but the cover rotated the image 45 degrees to make it more visually appealing. The contour is used on page 118 of the fourth edition to integrate rational functions along the positive real axis [1].
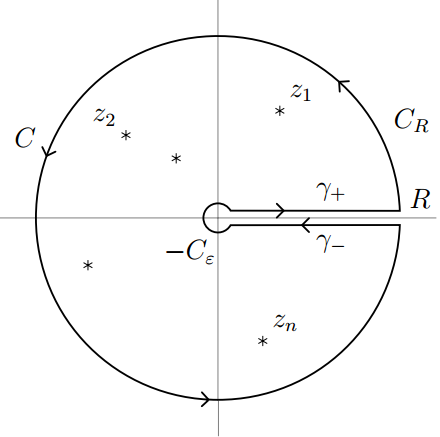
If the function you’re integrating has poles only at the locations marked by stars, then you can evaluate the integral around the contour by computing the residues of the integrand at these points. Now suppose you change the contour by making the outer circle larger, letting its radius R go to infinity, and making the inner circle shrink, letting its radius ε go to zero. If the integral along these two circular segments goes to zero in the limit, you’re left with the integral along the positive real axis.
Hankel
The keyhole contour is sometimes called the Hankel contour because Hermann Hankel used it in the 19th century to investigate special functions such as the gamma function and the eponymous Hankel functions. The first post in this series of book cover commentaries mentioned a book that has a plot of a Hankel function on the cover.
Related posts
[1] Specifically, Whittaker and Watson show how to compute the integral of xa−1 Q(x) from 0 to infinity, where Q is a rational function with no positive real zeros, and the limit of xa Q(x) is zero both as x goes to zero and as x goes to ∞.
