In base 10, four decibel values are approximately integers. Yesterday I explored whether base 10 was unique in this regard. I defined the value of n decibels in base b to be
g(n, b) = bn/b.
Sticking in 10 for b gives the usual definition of decibel levels.
There are two ways to quantify what proportion of (generalized) decibel values are near integers:
- Pick a tolerance value ε and count what proportion of values lie within ε of an integer.
- Measure the average distance of decibel values to integers.
The first approach is more natural, but the second approach is more convenient. Yesterday’s post focused on the latter. Today I’ll return to the former.
The problem with the first approach is that it depends on your choice of ε. Here’s a graph that shows what we get when we count the proportion of near integer decibel values for bases 2 through 1000 using three different values of ε.
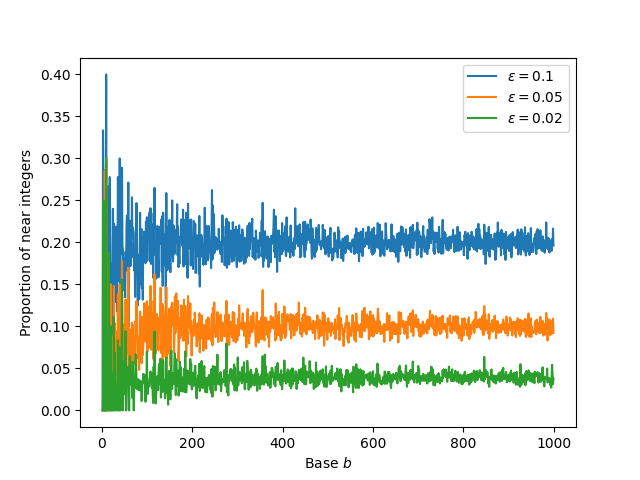
Naturally the smaller your value of ε, the stricter your notion of “near,” the smaller proportion of near integers you’ll find.
Notice that for large values of b the proportions jitter around the value 2ε. For large bases, the fractional parts of decibel levels behave like uniform random numbers between 0 and 1, and so the distance to the nearest integer behaves like a uniform random variable between 0 and 0.5. The probability such a value is less than ε equals ε/0.5 = 2ε.
For small values of b things are more interesting. The left side of the graph above shows a lot of overlap between the three plots. We see mostly green just because I plotted the green line last. Let’s zoom in on the bases up to 20.
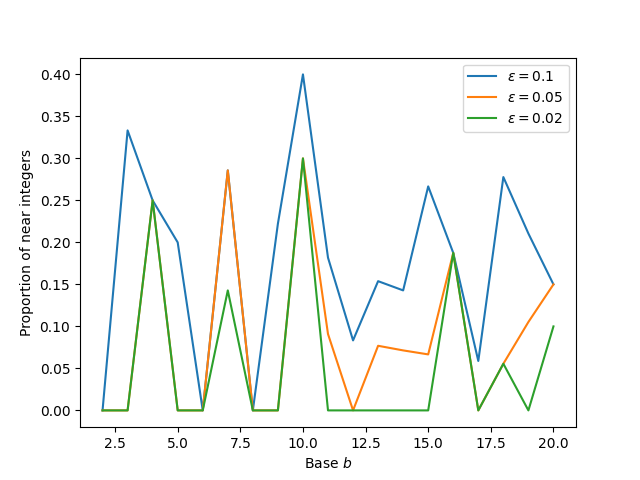
I first made this plot using discrete markers rather than connected lines. Generally that’s a good thing to do for functions only defined on integers. But the plot was hard to read. Connecting the lines makes it easier to see which values correspond to the same value of ε.
For each of the values of ε above, base 10 has the highest proportion of near integer decibel values. Which base has the second highest proportion depends on the value of ε.
If you pick ε small enough, i.e. smaller than the distance of any base 10 decibel value to an integer, then base 4 has the highest proportion of near integer decibels because one of its values is exactly and integer: in base 4, 2 dB equals 2. In the notation above, g(2, 4) = 2.
