A few days ago I wrote about Room squares, squares named after Thomas Room. This post will be about Room’s original square.
You could think of a Room square as a tournament design in which the rows represent locations and the columns represent rounds (or vice versa). Every team plays every other team exactly once, and only one pair of teams can play each other at the same location in the same round.
Here is an image creating from Room’s original square using the visualization approach from the earlier post.

This is not a trivial variation on the square in the earlier post. Notice that this square has a block of four contiguous squares in the middle row and middle column. The previous image does not.
Here is Room’s original square, presented as in his half-page announcement in [1] with the rows and columns labeled with binary numbers.
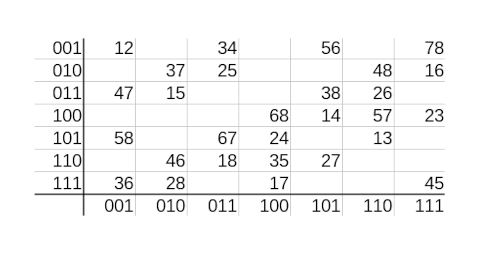
A plain text version of the image above is available below [2].
Room points out an interesting pattern: a cell is filled in if and only if the “dot product” of its coordinate is odd. Think of each coordinate number as three dimensional vector and take the dot product of the vector representing the row and the vector representing the column.
Room didn’t refer to dot products. In his words
(αβγ, λμν) are the coordinates of one of the points marked rs in and only if αλ + βμ + γν is odd.
Related posts
[1] T. G. Room. A new type of magic square. Mathematical Gazette. Volume 39 (1955), p. 307.
[2] Here is Room’s square as a plain text (org-mode) table.
|-----+-----+-----+-----+-----+-----+-----+-----| | 001 | 12 | | 34 | | 56 | | 78 | | 010 | | 37 | 25 | | | 48 | 16 | | 011 | 47 | 15 | | | 38 | 26 | | | 100 | | | | 68 | 14 | 57 | 23 | | 101 | 58 | | 67 | 24 | | 13 | | | 110 | | 46 | 18 | 35 | 27 | | | | 111 | 36 | 28 | | 17 | | | 45 | |-----+-----+-----+-----+-----+-----+-----+-----| | | 001 | 010 | 011 | 100 | 101 | 110 | 111 | |-----+-----+-----+-----+-----+-----+-----+-----|
