The earth’s orbit around the sun is nearly a circle, and the moon’s orbit around the earth is nearly a circle, but what is the shape of the moon’s orbit around the sun?
You might expect it to be bumpy, bending inward when the moon is between the earth and the sun and bending output when the moon is on the opposite side of the earth from the sun. But in fact the shape of the moon’s orbit around the sun is convex as proved in [1] and illustrated below.
If the moon orbited the earth much faster, say 10 times faster, at the same altitude, then we see that the orbit is indeed bumpy.
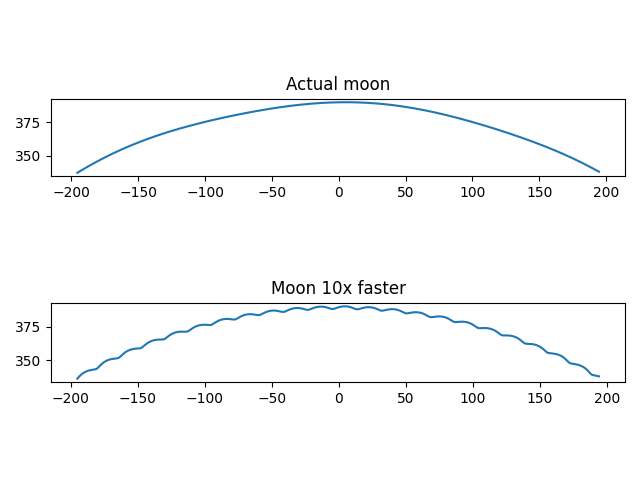
However, the nothing could orbit the earth 10x faster than the moon at the same distance as the moon. Orbital period determines altitude and vice versa.
A more realistic example would be a satellite in MEO (Medium Earth Orbit) like a GPS satellite. Such a satellite orbits the earth roughly twice a day. The path of a MEO satellite around the sun is not convex.
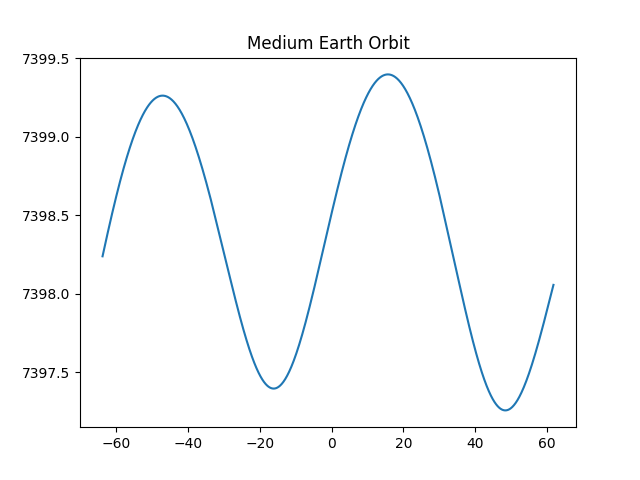
The plot above shows about one day of an MEO satellite’s orbit around the sun. Note that the vertical and horizontal scales are not the same; it would be hard to see anything but a flat line if the scales were the same because the satellite is far closer to the earth than the sun.
Here are the equations from [1]. Choose units so that the distance to the moon or satellite is 1 and let d be the distance from the planet to the sun. Let p be the number of times the moon or satellite orbits the planet as the planet orbits the sun (the number of sidereal periods).
x(θ) = d cos(θ) + cos(pθ)
y(θ) = d sin(θ) + sin(pθ)
This assumes both the planet’s orbit around the sun and the satellite’s orbit around the planet are circular, which is a good approximation in our examples.
[1] Noah Samuel Brannen. The Sun, the Moon, and Convexity. The College Mathematics Journal, Vol. 32, No. 4 (Sep., 2001), pp. 268-272
