The nine-point circle theorem says that for any triangle, there is a circle passing through the following nine points:
- The midpoints of each side.
- The foot of the altitude to each side.
- The midpoint between each vertex and the orthocenter.
The orthocenter is the place where the three altitudes intersect.
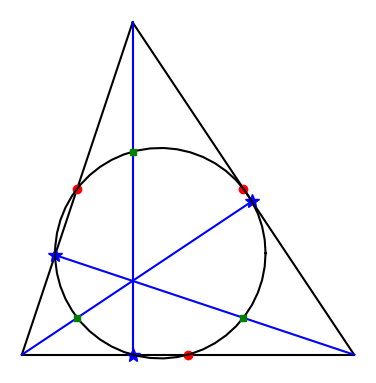
In the image above, the midpoints are red circles, the altitudes are blue lines, the feet are blue stars, and the midpoints between the vertices and the orthocenter are green squares.

D. Pedoe, CIRCLES, A Mathematical View begins with that beautiful result, but according to Pedoe, Feuerbach’s theorem is The nine-point circle of a triangle touches the incircle and excircles of the triangle