A few days ago I wrote about the law of cotangents. This law says that if we label the sides of a triangle a, b, c and label the angles opposite each side α. β, γ, then
where s is the semi-parameter, i.e.
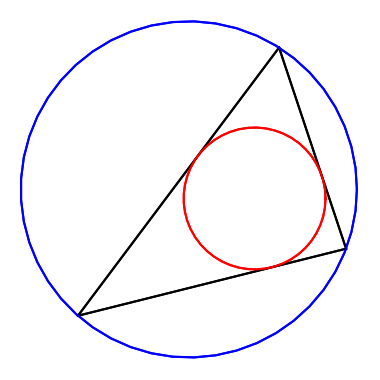
and r is the radius of the incircle, the largest circle that can be inscribed in the triangle. This is the red circle in the image above.
The law of sines is sort of a dual to the law of cotangents. Just as the law of cotangents gives you the radius of the inscribed circle, the law of sines gives you the radius of the circumcircle, the blue circle in the image above. That is,
where d is the diameter of the circle through the vertices of the triangle.
