A few days ago a comment that a graph looked like a Maxwell-Boltzman density lead to an approximation of 1/Γ(x), possibly a useful approximation.
Approximating Γ(x) is a well-known problem, and for large x the solution is to use Stirling’s approximation or a few more terms from the asymptotic series that Stirling’s approximation is a part of. But is the reciprocal of a good approximation to Γ(x) a good approximation to 1/Γ(x)? To put it visually, does the following diagram commute?
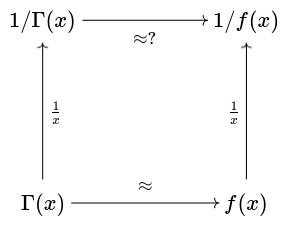
To make this question precise we have to say more about what we mean by a good approximation. If we’d like to minimize relative error, then the diagram does commute: if the ratio f/g is close to 1, then the ratio g/f is close to 1.
But let’s assume we want to minimize absolute error in some sense: maybe maximum absolute error, or the integral of (some power of) absolute error. That’s what we were implicitly doing in the earlier post when we were eyeballing plots of 1/Γ(x) and its approximation. Even though approximating Γ(x) with respect to relative error is a solved problem, that doesn’t mean that approximating 1/Γ(x) with respect to absolute error is a solved problem.
The relative error in Stirling’s approximation is good for large x, and gets better as x gets larger. But while the relative error decreases, the absolute error increases.
This means that Stirling’s approximation shines when we don’t need it to shine. It minimizes the relative error in approximating 1/Γ(x) precisely when 1/Γ(x) is so small that simply approximating it with 0 would give good absolute error.
***
Let’s revisit the earlier post and go into more detail. In that post we scaled 1/Γ(x) so that it integrated to 1, then we approximated the result by the PDF of a chi distribution with k degrees of freedom that has the same mode. We found that k = 3, corresponding to the Maxwell-Botlzmann distribution, doesn’t do a very good job, but k = 2 or a little smaller does much better. I said that k= 1.86 looked like a good fit.
This morning I computed the approximation error in Lp norm for a variety of values of p. For p = 1 and p = 2 the error is minimized for k approximately 1.9. For p = 10 the minimum is close to 2. So if you want to minimize the RMS (root mean square) error, you’d pick p = 1.9, and if you want to minimize the maximum error, you’d pick p = 2.
Here’s a plot of the error in approximating c/Γ(x) with a chi distribution with 2 degrees of freedom, scaled to match modes.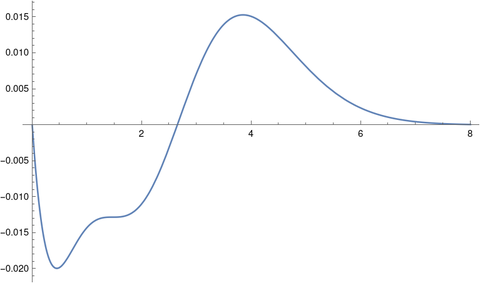
This says that the function 1/Γ(x) is decently approximated by 2.80777 times the density of a chi random variable with 2 degrees of freedom and scale 1.46163. The factor of 2.80777 is the integral of 1/Γ(x) from 0 to ∞ and the scale comes from matching modes.
