The previous post discussed the circumcenter and orthocenter of a triangle. Euler proved that the centroid, circumcenter, and orthocenter all fall on a common line, now called the Euler line.
The centroid is the center of mass of a triangle. If you draw lines from each vertex to the midpoint of the opposite side, the three lines intersect at the centroid.
The center of the nine-point circle also lies on the Euler line, though this was discovered after Euler.
Trilinear coordinates
Let α. β, and γ denote the three angles of the triangle.
The previous post said that the trilinear coordinates, of the circumcenter are
cos α : cos β : cos γ
and the trilinear coordinates of the orthocenter are
sec α : sec β : sec γ.
The trilinear coordinates of the centroid are
csc α : csc β : csc γ.
The center of the nine-point circle has trilinear coordinates
cos β-γ : cos γ-α : cos α-β.
Here’s a visualization for a particular triangle.
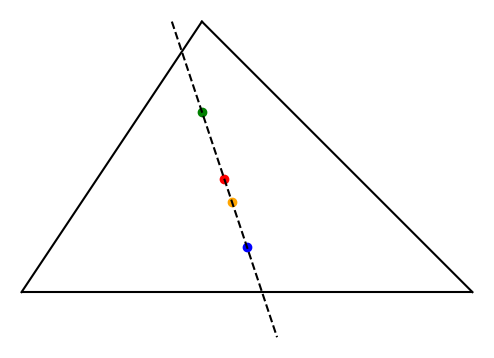
The dashed line in the figure above is the Euler line for a particular triangle. The colored dots, moving from northwest to southeast, are the orthocenter, nine-point center, centroid, and circumcenter.
For an equilateral triangle, all four of these points coincide.
Proof outline
Discovering the Euler line required a flash of insight. Verifying it does not.
Three points are colinear if the 3×3 matrix formed by stacking their trilinear coordinates has zero determinant. So we could prove Euler’s original theorem by showing that the determinant of the matrix
is zero. This isn’t zero for arbitrary α, β, and γ. But since these are angles in a triangle,
γ = π – α – β
and with that additional information we can show that the determinant is zero. We could replace one of the rows with the trilinear coordinates of the nine-point circle to show that it also lies on the Euler line.
