Suppose you hire me to solve an optimization problem for you. You want me to find the value of x that minimizes f(x). I go off and work on finding the best value of x. I report back what I found, and you might say “Thanks, That’s a good value of x. But how do I know there’s not an even better value?”
In general this is a hard question to answer. If x were a single number, maybe I could produce a plot of f and show that my x is where f takes on its smallest value. But usually x is a vector, maybe a thousand-dimensional vector. I’m not very good at graphing functions in a thousand dimensions, so this approach isn’t going to work.
I may be able to back up my result by defending the process used to produce it. For example, maybe you ask me for the shortest path through the 254 counties in Texas and I come back with the following tour:
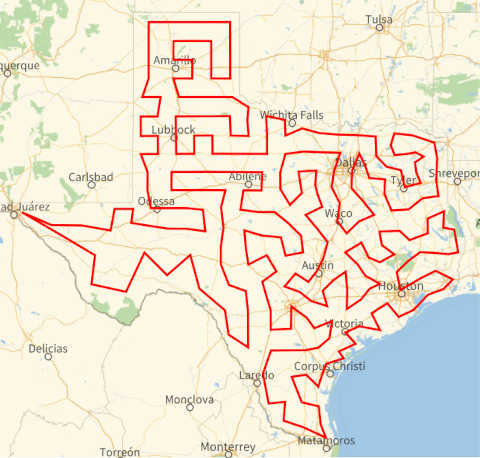
If you ask whether this is optimal, I’ll have to admit that I’m not certain that it is, but I am certain that it is close. The tour was produced using Mathematica, which in turn uses Bill Cook’s Concorde algorithm, which is known to produce near-optimal results. If the tour above isn’t the shortest, the shortest tour isn’t much shorter.
But if the optimization problem is convex then you may be able to certify the result analogous to the way you can certify primes. In general a certificate gives you a way to verify a solution with much less effort than it took to find the solution.
You can prove things by moving back and forth between your original (“primal”) problem and its dual, or between a variation of your original problem and its dual. You may be able to certify that no solution to the constraints of the original problem exists, or certify that a proposed solution is or isn’t optimal. In every case, demonstrating one solution to the dual problem proves something about all solutions to the primal problem.

So, how short is the distance of the path through Texas in your article?