An ellipse can be defined as the set of points such that the sum of the distances to two fixed points, the foci, has a constant value.
A Cassini oval is the set of points such that the product of the distances to two foci has a constant value.
You can write down an equation for a Cassini oval for given parameters a and b as
((x + a)² + y²) ((x – a)² + y²) = b².
For some reason, references almost always plot Cassini ovals by fixing a and letting b vary. When we set a = 1 and let b = 0.5, 1, 1.5, …, 5 this produces the following plot.
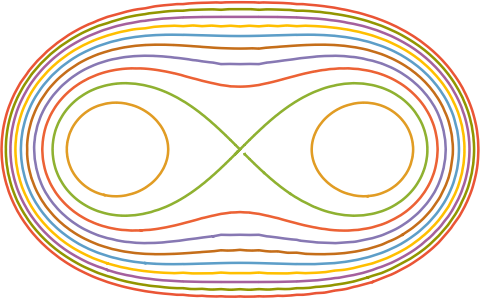
But you could also fix b and let a vary. Here’s what we get when we set b = 1 and let a = 0, 0.1, 0.2, …, 1.
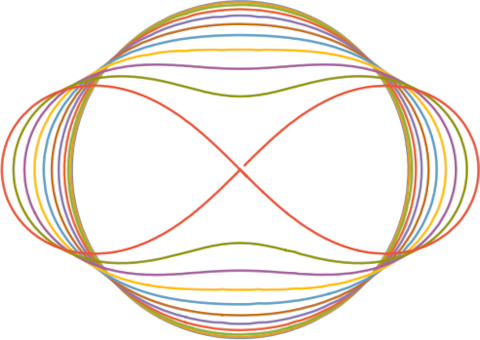
Incidentally, the red figure eight in the middle, corresponding to a = 1, is known as the lemniscate, or more formally the lemniscate of Bernoulli.
