Johannes Kepler thought that planetary orbits were ellipses. Giovanni Cassini thought they were ovals. Kepler was right, but Cassini wasn’t far off.
In everyday speech, people use the words ellipse and oval interchangeably. But in mathematics these terms are distinct. There is one definition of an ellipse, and several definitions of an oval. To be precise, you have to say what kind of oval you have in mind, and in the context of this post by oval I will always mean a Cassini oval.
Ellipses and ovals each have two foci, f1 and f2. Let d1(p) and d2(p) be the distances from a point p to each of the foci. For an ellipse, the sum d1(p) + d2(p) is constant. For an oval, the product d1(p) d2(p) is constant.
In [1] the authors argue that just as planetary orbits are nearly circles, they’re also nearly ovals. This post will look at how far the earth’s orbit is from a circle and from an oval.
We need a way to specify which oval we want to compare to the ellipse of earth’s orbit. We’ll do this by equating the major and minor semi-axes of the two curves. These are usually denoted a and b, but the same variables have a different meaning in the context of ovals, so I’ll denote them by M for major and m for minor.
The equation of an ellipse is
(x/M)² + (y/m)² = 1
and the equation of an oval is
((x + a)² + y²) ((x – a)² + y²) = b².
Setting x = 0 in the equation of an oval tells us
m² = b – a²
and setting y = 0 tells us
M² = b + a².
So
b = (M² + m²)/2
and
a² = (M² – m²)/2.
For the earth’s orbit, M = 1.00000011 and m = 0.99986048 measured in AU, astronomical units. So or oval has parameters
a = 0.011816102
and
b = 0.99986060.
If you plot Kepler’s ellipse and Cassini’s oval for earth’s orbit at the same time, you can’t see the difference.
Planet orbits are nearly circular. If we compare a circle of radius 1 AU with Kepler’s ellipse we get a maximum error of about 1 part in 10,000.
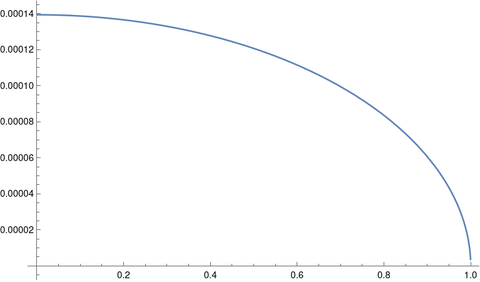
But if we compare Cassini’s oval with Kepler’s ellipse we get a maximum error of about 1 part in 100,000,000.
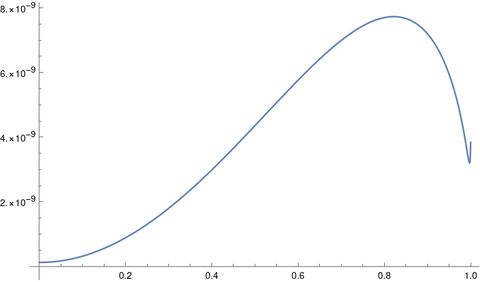
In short, a circle is a good approximation to earth’s orbit, but a Cassini oval is four orders of magnitude better.
It would be difficult to empirically distinguish an ellipse from an oval as the shape of earth’s orbit, but theory is clearly on Kepler’s side since his ellipses fall out of Newton’s laws. Cassini’s error was more qualitative than quantitative.
More orbital mechanics posts
[1] Kepler’s ellipse, Cassini’s oval and the trajectory of planets. B Morgado1 and V Soares. 2014 Eur. J. Phys. 35 025009 DOI 10.1088/0143-0807/35/2/025009
