Quasiperiodic functions

This post will distinguish between periodic, almost periodic, and quasiperiodic functions, and give examples of the latter.

Definitions

A function f is periodic with period T if

f(x + T) = f(x)

for all x. For example, trig functions are periodic.

A function f is almost periodic with period T if

f(x + T) ≈ f(x)

for all x. More precisely, given a tolerance ε, you can find a value of T depending on ε such that the two sides of the approximation are within ε of each other. See this post for a little more detail and an example.

A function f is quasiperiodic if

f(x + T) = g(x, f(x))

for all x, where g is a “simple function.” Exactly what it means for a function to be “simple” is not defined, and so quasiperiodic is an umbrella term for multiple ideas of what it means for a function to be quasiperiodic.

Comparing almost periodic and quasiperiodic

Both the word “almost” and the prefix “quasi” mean that what follows doesn’t exactly hold, but it sorta holds. In the case of almost periodic functions, periodicity almost holds in the sense that function values at shifted points are numerically close to the values at the original point. Quasiperiodic functions satisfy a condition that is a variation on periodicity.

To put it another way, almost periodic functions approximately satisfy the exact definition of periodicity, while quasiperiodic functions exactly satisfy a variation of the definition.

Example: Gamma function

Let the function g in the definition of quasiperiodic be the function that multiplies its two arguments, and let T = 1. This special case of a quasiperiodic function is a function that satisfies

f(x + 1) = x f(x).

This is the equation that the gamma function Γ(x) satisfies, so the gamma function is quasiperiodic.

Example: Exponential sums

Now let g(w, z) = z + C for some constant C. I wrote about a function that is quasiperiodic with this g last Fall. See Smoothly extending arctan(k tan(t)).

The exponential sum of the day has the same kind of quasiperiodicity. Sometimes C = 0 and the function is periodic, and other times the function repeats itself but shifted by a constant.

Today’s exponential sum is periodic:

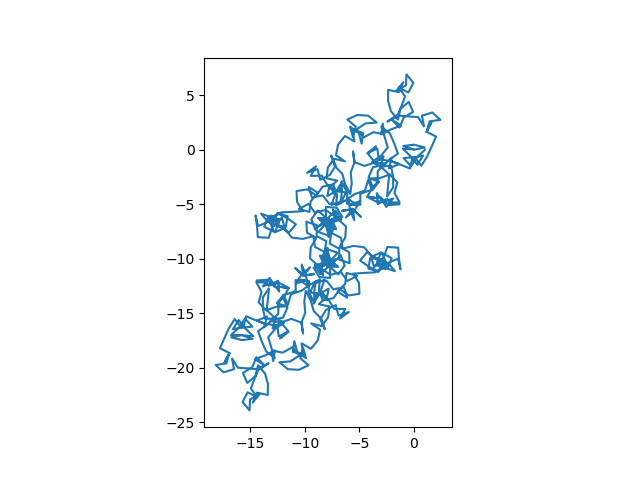
The exponential sum from 11/26/22 was quasiperiodic but not periodic.

The exponential sum of the day plots the partial sums of

where m, d, and y are the month, day, and the two-digit year. The terms of the sum are periodic functions of n with period T equal to the least common multiple of m, d, and y. (This gives us a period, but perhaps not the smallest period. In the example above, the smallest period is T/2.)

The partial sums are a quasiperiodic function of N with quasiperiod T. The constant C is equal to the sum up to N = T – 1.

In the preceding example, T = lcm(11, 26, 22) = 286, and the smallest period is T′ = 143. The constant C for quasiperiod T′ is 7.573. (Note that the value of C depends on which period you choose.)

In this example C happens to be a real number, but in general C is complex, and so the pattern may repeat at any angle and not just horizontally. See, for example, the exponential sum for 11/28/22.

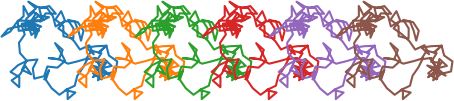
Here’s the plot above again, but with each quasiperiod plotted in a different color.