The sinc function is defined either as sin(x)/x or as sin(πx)/πx. We’ll use the former definition here because we’ll cite a paper that uses that definition.
Here’s a plot of the sinc function and its first two derivatives.
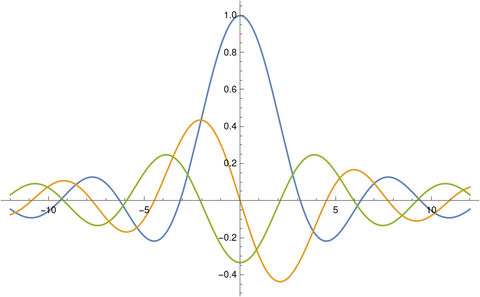
Thomas Grönwall proposed a problem to the American Mathematical Monthly in 1913 [1] bounding the derivatives of the sinc function:
Seven years later, Dunkel gave an elegant proof. Perhaps Grönwall had a proof and was proposing his inequality as a challenge, or maybe it was a conjecture at the time he published it. In any case, the proof by Dunkel is very nice. He sets
y = sin(x)/x
and repeatedly differentiates both sides of the equation
xy = sin(x).
See the details in Dunkel’s solution.
I don’t know of an application of Grönwall’s inequality offhand. But the sinc function is common in signal processing, and so maybe his inequality has applications there.
(By “Grönwall’s inequality” I mean the inequality above. There is another theorem also known as Grönwall’s inequality that is commonly applied in differential equations.)
[1] Gronwall, T. H. (1913). Problem 339. Amer. Math. Monthly. 20: 196.
[2] Dunkel, O., (1920). Solution to Problem 339. Amer. Math. Monthly. 27: 81–85.
