Another Napoleon-like theorem

A little while back I wrote about Napoleon’s theorem for triangles. A little later I wrote about Van Aubel’s theorem, a sort of analogous theorem quadrilaterals. This post presents another analog of Napoleon’s theorem for quadrilaterals.

Napoleaon’s theorem says that if you start with any triangle, and attach equilateral triangles to each side, the centroids of these new triangles are the vertices of an equilateral triangle.

So if you attach squares to the sides of a quadrilateral, are their centroids the vertices of a square? In general no.

But you can attach squares to two sides, and special rectangles to the other two sides, and the centroids will form the corners of a square. Specifically, we have the following theorem by Stephan Berendonk [1].

If you erect squares on the two “nonparallel” sides of a trapezoid and a rectangle on each of the two parallel sides, such that its “height” is equal to the length of the opposite side of the trapezoid, then the centers of the four erected quadrangles will form the vertices of a square.

Here’s an illustration. Berendonk’s theorem asserts that the red quadrilateral is a square.

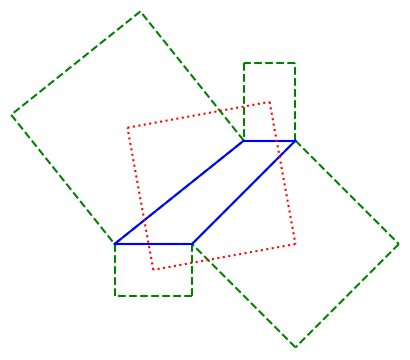
[1] Stephan Berendonk. A Napoleonic Theorem for Trapezoids. The American Mathematical Monthly, April 2019, Vol. 126, No. 4, pp. 367–369