The Gumbel distribution, named after Emil Julius Gumbel (1891–1966), is important in statistics, particularly in studying the maximum of random variables. It comes up in machine learning in the so-called Gumbel-max trick. It also comes up in other applications such as in number theory.
For this post, I wanted to point out how a couple famous constants are related to the Gumbel distribution.
Gumbel distribution
The standard Gumbel distribution is most easily described by its cumulative distribution function
F(x) = exp( −exp(−x) ).
You can introduce a location parameter μ and scale parameter β the usual way, replacing x with (x − μ)/β and dividing by β.
Here’s a plot of the density.
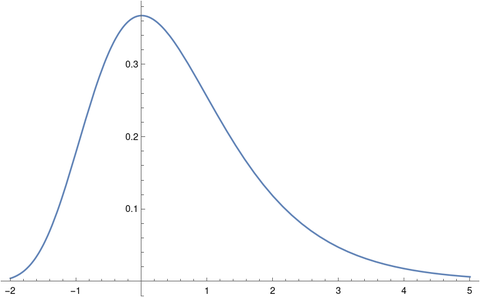
Euler-Mascheroni constant γ
The Euler-Mascheroni constant γ comes up frequently in applications. Here are five posts where γ has come up.
- Numbers worth memorizing
- The coupon collector problem
- Pratt prime proofs
- Distribution of Mersenne primes
- Average fraction round up
The constant γ comes up in the context of the Gumbel distribution two ways. First, the mean of the standard Gumbel distribution is γ. Second, the entropy of a standard Gumbel distribution is γ + 1.
Apéry’s constant ζ(3)
The values of the Riemann zeta function ζ(z) at positive even integers have closed-form expressions given here, but the values at odd integers do not. The value of ζ(3) is known as Apéry’s constant because Roger Apéry proved in 1978 that ζ(3) is irrational.
Like the Euler-Mascheroni constant, Apéry’s constant has come up here multiple times. Some examples:
The connection of the Gumbel distribution to Apéry’s constant is that the skewness of the distribution is
12√6 ζ(3)/π³.
