Suppose a planet is in an elliptical orbit around the sun with semimajor axis a and semiminor axis b. Then the average distance of the planet to the sun over time equals
a(1 + e²/2)
where the eccentricity e satisfies
e² = 1 − b²/a².
You can find a proof of this statement in [1].
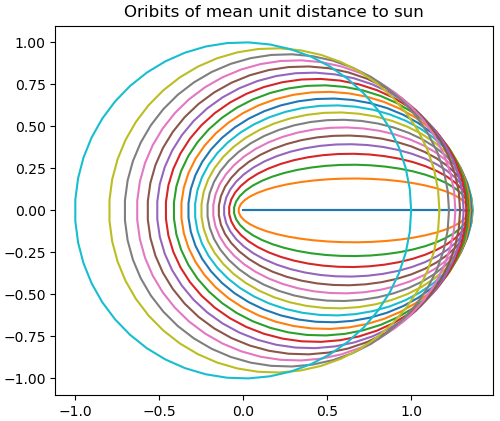
This post will look at the set of all orbits with a fixed average distance r to the sun. Without loss of generality we can choose our units so that r = 1.
Clearly one possibility is to set a = b = 1 so the orbit is a circle. The distance is constantly 1, so the average is 1.
We can also maintain a distance of 1 by reducing a but increasing the eccentricity e. The possible orbits of average distance 1 satisfy
a(1 + e²/2) = 1
with 0 < b ≤ a ≤ 1. A little algebra shows that
b = √(3a² – 2a),
and that 2/3 < a ≤ 1. As a approaches 2/3, b approaches 0.
Let’s put the center of our coordinate system at the sun and assume the other focus of the elliptical orbits is somewhere along the positive x-axis. When e is 0 we have a unit circle orbit. As e approaches 1, the orbits approach a horizontal line with the sun on one end.
Related posts
[1] Sherman K. Stein. “Mean Distance” in Kepler’s Third Law. Mathematics Magazine, Vol. 50, No. 3 (May, 1977), pp. 160–162
