The previous post discussed the functions
as test cases for plotting. This post will look at using the same functions as test cases for integration. As you can see from the plot of f30(x) below, the function is continuous, but the derivative of the function has a lot of discontinuities.
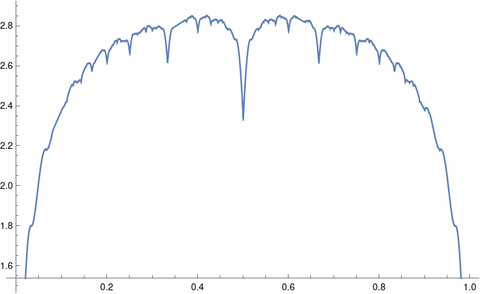
The integrals of Steinerberger’s functions can be computed easily in closed form. Each term in the sum integrates to 2/πk and so
where Hn is the nth harmonic number.
Symbolic integration
When I tried to get Mathematica to compute the integral above for general n it got stuck.
When I tried the specific case of 10 with
Integrate[f[x, 10], {x, 0, 1}]
it churned for a while, then returned a complicated expression involving nested radicals:
(1/(79380 \[Pi]))(465003 + 400 Sqrt[2 (48425 - 13051 Sqrt[5])] -
35600 Sqrt[2 (5 - Sqrt[5])] + 42800 Sqrt[2 (5 + Sqrt[5])] -
400 Sqrt[2 (48425 + 13051 Sqrt[5])])
Mathematica could not simplify the result to
HarmonicNumber[10] 2/Pi]
but it could confirm that the two expressions are numerically equal within the limitations of floating point precision.
Assuming the two expressions for the integral are equal, it would be interesting to see why this is so. I don’t see off hand where the radicals above come from.
Numerical integration
When I asked Mathematica to compute the integral above numerically with
NIntegrate[f[x, 10], {x, 0, 1}]
it produced an answer which correct to four decimal places and a warning
NIntegrate failed to converge to prescribed accuracy after 9 recursive bisections in x near {x} = {0.667953}. NIntegrate obtained 1.8646445043323603` and 2.908590085997311`*^-6 for the integral and error estimates.
Even though NIntegrate didn’t achieve full precision, it warned that this was the case. It produced a decent answer and a fairly good estimate of its error, about half of the actual error.
I tried numerically integrating the same function with Python.
from scipy.integrate import quad
quad(lambda x: f(x, 10), 0, 1)
Python’s quad function did about the same as Mathematica’s NIntegrate. It produced the following warning:
IntegrationWarning: The maximum number of subdivisions (50) has been achieved. If increasing the limit yields no improvement it is advised to analyze the integrand in order to determine the difficulties. If the position of a local difficulty can be determined (singularity, discontinuity) one will probably gain from splitting up the interval and calling the integrator on the subranges. Perhaps a special-purpose integrator should be used. (1.8646395747766926, 0.0024098799348653954)
This error message is more helpful, and the error estimate 0.0024 is an upper bound on the error.
Increasing the number of subdivisions by a factor of 10 with
quad(lambda x: f(x, 10), 0, 1, limit=500)
eliminated the warning and made the integration much more accurate.

The Simplify function is meant to be used to do very elemental simplifications. To most interesting simplifications one should use FullSimplify. In this case, for example, FullSimplify[(1/(79380 \[Pi]))(465003 + 400 Sqrt[2 (48425 – 13051 Sqrt[5])] – 35600 Sqrt[2 (5 – Sqrt[5])] + 42800 Sqrt[2 (5 + Sqrt[5])] – 400 Sqrt[2 (48425 + 13051 Sqrt[5])])] does work.
Thanks. I thought I’d tried FullSimplify but apparently I didn’t.