Here’s a graphical way to multiply two positive numbers a and b using the parabola y = x².
- Start at the origin, move a units to the left, then go up vertically to the parabola, and draw a point.
- Go back to the origin, move b units to the right, go up vertically to the parabola, and draw another point.
- Connect the points and see where they cross the y-axis. That point is ab.
Here’s an example multiplying 3 and 5.
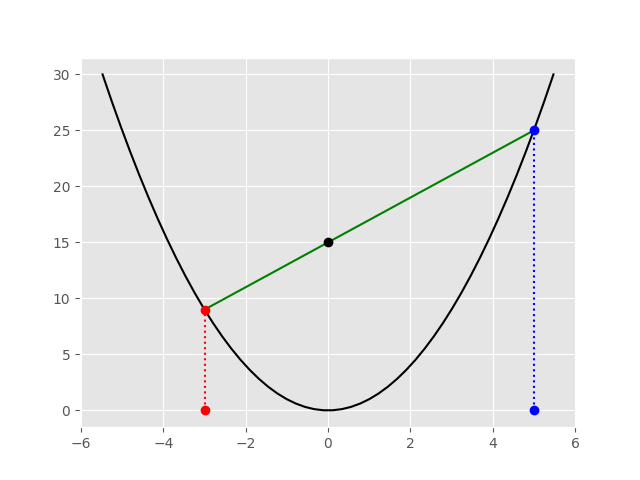
Here’s why this works. The slope of the line is the change in y over the change in x which is
m = (b² − a²)/(b − (−a)) = b − a.
Use the equation of a line
y − y0 = m(x – x0)
with x0 = b and y0 = b² to get
y − b² = (b − a)(x − b).
Stick in x = 0 and you get y = ab.

There is a quite nice application of this property: the Parabolic Sieve of prime numbers!
I liked it! I will teach it to my students when they learn about parabolas.
Reminds me of how Babylonians multiplied numbers using square tables using the identity ab=½[(a+b)²−a²−b²], because regular multiplication tables are impractical for base 60.
https://mathshistory.st-andrews.ac.uk/HistTopics/Babylonian_mathematics/
@Michael: I think some mental calculators use that identity too.
Is this the method used to multiply two numbers in the spiral staircase at the National Museum of Mathematics in New York City? It looks like this: https://momath.org/wp-content/uploads/2016/01/dsc_0368_2.jpg
Nice
@ Michael Scharrer…dear Sir i found same type method for multiplication used by Aryabhat too( indian mathematician astronomer born 476 CE