I recently stumbled across the identity
while reading [1]. Here ⌊x⌋ is the floor of x, the largest integer not larger than x.
My first thought was that this was hard to believe. Although the floor function is very simple, its interactions with other functions tends to be complicated. I was surprised that such a simple equation was true.
My second thought was that the equation makes sense. For large n the three terms on the left are roughly equal, and so
Not only that, the approximation gets better as n gets larger. So the theorem is at least plausible.
My third thought was that there is something subtle going on here. Why the 8 on the right hand side? It turns out the theorem is false if you replace the 8 with a 9. Equality fails to hold for n = 0, 3, 8, 15, …
There is a difference between saying x ≈ y and saying ⌊x⌋ = ⌊y⌋. The former makes the latter plausible, but it’s not the same. If x and y are very close, but on opposite sides of an integer, then ⌊x⌋ ≠ ⌊y⌋.
In fact, the approximation
is better when a = 9 than when a = 8. Here’s a plot of the approximation errors.
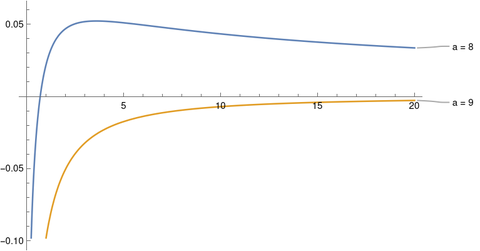
So there’s something clever going on with the selection a = 8.
According to [1], the equation at the top was proposed as a problem in 1988 and a solution was published in 2005. The time span between the proposed theorem and its proof suggests that the proof isn’t trivial, though I have not yet read it.
This is an obscure problem, and so we can’t assume that hundreds of mathematicians were feverishly trying to find a solution for 17 years. On the other hand, if there were a trivial proof it seems someone would have posted it quickly.
[1] Prapanpong Pongsriiam. Analytic Number Theory for Beginners, 2nd edition.. American Mathematical Society 2023

Nice. I added a link to this page to https://oeis.org/A114458
I don’t know about _trivial_, but it’s not hard to prove.
First of all, it’s a bit tidier to offset n by 1, so we want to show that sqrt(9n-1) and sqrt(n-1) + sqrt(n) + sqrt(n+1) have the same integer part. That’s the same as there being no integer between them. I claim that in fact sqrt(9n-1) < sqrt(n-1) + sqrt(n) + sqrt(n+1) < sqrt(9n), so not only is there no _integer_ in between, there is no _square root of an integer_ in between. (Obviously every integer is also the square root of an integer.)
The comparison with sqrt(9n) = 3 sqrt(n) is a trivial application of convexity, so we need only show that
9n-1 <= 3n + 2 sqrt(n^2-n) + 2 sqrt(n^2-1) + 2 sqrt(n^2+n).
Rearranging a bit, this is equivalent to
6-1/n <= 2 sqrt(1-1/n) + 2 sqrt(1-1/n^2) + 2 sqrt(1+1/n)
or, writing x = 1/n, to
6-x = 4-2x+x^2/4, which is true if 17/4.x^2 <= 2x, which is true if x = 16 – 4x + x^2/4 or 8 sqrt(1-x^2) >= 8 – 4x + x^2/4. If x = 8-2x; this implies the result we’re looking for provided we also have 2x >= x^2/4 or x <= 1/8.
So everything works provided x = 8, and it’s easy to check smaller n by hand.
The above sum is in fact floor(sqrt(9*n+7)) because for every integer n, floor(sqrt(9*n+8)) = floor(sqrt(9*n+7)).
To see this is true, we note that if m is an integer, then either floor(sqrt(m−1)) = floor(sqrt(m)) − 1 or floor(sqrt(m−1)) = floor(sqrt(m)). The former happens if m is a perfect square, the latter if m is not.
We next show that 9*n+8 is never a perfect square. Consider the arithmetic progressions 9*n, 9*n+1, 9*n+2, …, 9*n+8. Every integer is in one of these sequences, and so the square of every integer is congruent mod 9 to 0, 1, 4, or 7. For instance, (9*n+4)^2 = 9*(9*n^2 + 8*n + 1) + 7 ≡ 7 mod 9. On the other hand, obviously every integer 9*n+8 ≡ 8 mod 9, and hence no such integer is a perfect square. To wrap up, we use the result in the first paragraph to conclude that floor(sqrt(9*n+8)) = floor(sqrt(9*m+7)).
Something has obviously gone very wrong with my comment above; I suspect that what’s happened is that some things involving less-than signs have been stripped out for HTML-related reasons. (Obvious conjecture: every minimal instance of LESS-THAN (… stuff …) GREATER-THAN has been removed. I’m not sure whether this conjecture is consistent with the garbled comment-text that remains.)
I don’t know remember exactly how the missing bits of argument went, but it will have been something along the following lines. We want 6-x <= 2 sqrt(1-x) + 2 sqrt(1-x^2) + 2 sqrt(1+x). First of all, by way of motivation, the RHS is an even function of x, so its Taylor series has no odd-exponent terms, so it begins 6 + (no x) + something x^2, so for small x it has to be bigger than 6-x.
So we just need some explicit bounds on how much smaller these sqrt() things can be than the early terms in their Taylor series, when x is fairly small (as it is once n isn't small, since x = 1/n). So e.g. we can look for inequalities like sqrt(1-x^2) GE 1 – t x^2 and sqrt(1-x) + sqrt(1+x) GE 1 – u x^2 where I am writing GE instead of the greater-than-or-equal sign in the hope of not having my formulae eaten by the blog software. Then we'll square both sides once or twice, rearrange, etc., and get conditions that end up looking like x <= some function of t and/or u. And then we just need 6 – x <= 6 – 2(t+u) x^2, which again is true provided x <= 1/2(t+u). We then pick any values of t,u, see what the most stringent of our inequalities requires of x, and then all is well provided n is large enough that x = 1/n is small enough. (And then check smaller n by hand.)