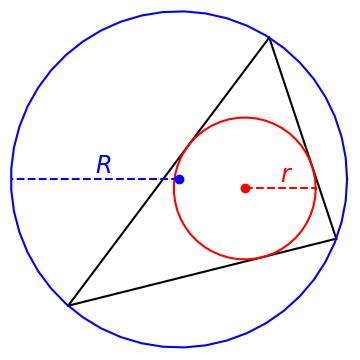
Suppose a triangle T has sides a, b, and c.
Let s be the semi-perimeter, i.e. half the perimeter.
Let r be the inner radius, the radius of the largest circle that can fit inside T.
Let R be the outer radius, the radius of the smallest circle that can enclose T.
Then three simple equations relate a, b, c, s, r, and R.
Given a, b, and c, use the first equation to solve for s, then the third equation for Rr, then the second for r, then go back to the last equation to find R.
Given s, r, and R, you can calculate the right hand sides of the three equations above, which are the coefficients in a cubic equation for the sides a, b, and c.
Note that this last statement is not about triangles per se. It’s a consequence of
which would be true even if a, b, and c were not the sides of a triangle. But since they are sides of a triangle here, the coefficients can be interpreted in terms of geometry, namely in terms of perimeter, inner radius, and outer radius.
