Very often when a number is large, and we don’t know or care exactly how large it is, we can model it as infinite. This may make no practical difference and can make calculations much easier. I give several examples of this in the article Infinite is easier than big.
When you run across a statement that something is infinite, you can often mentally replace “infinite” with “big, but so big that it doesn’t matter exactly how big it is.” Conversely, the term “finite” in applied mathematics means “limited in a way that matters.”
But when we say something does or does not matter, there’s some implicit context. It does or does not matter for some purpose. We can get into trouble when we’re unclear of that context or when we shift contexts without realizing it.
Zipf’s law
Zipf’s law came up a couple days ago in a post looking at rare Chinese characters. That post resolves a sort of paradox, that rare characters come up fairly often. Each of these rare characters is very unlikely to occur in a document, and yet collectively its likely that some of them will be necessary.
In some contexts we can consider the number of Chinese characters or English words to be infinite. If you want to learn English by first learning the meaning of every English word, you will never get around to using English. The number of words is infinite in the sense that you will never get to the end.
Zipf’s law says that the frequency of the nth word in a language is proportional to n−s. This is of course an approximation, but a surprisingly accurate approximation for such a simple statement.
Infinite N?
The Zipf probability distribution depends on two parameters: the exponent s and the number of words N. Since the number of words in any spoken language is large, and its impossible to say exactly how large it is, can we assume N = ∞? This seems like exactly the what we were talking about at the top of this article.
Whether it is possible to model N as infinite depends on s. The value of s that models word frequency in many languages is close to 1. The plot below illustrates Zipf’s law for the text of Wikipedia in many different languages. In each case, the slope on the log-log plot is approximately 1, i.e. s ≈ 1.
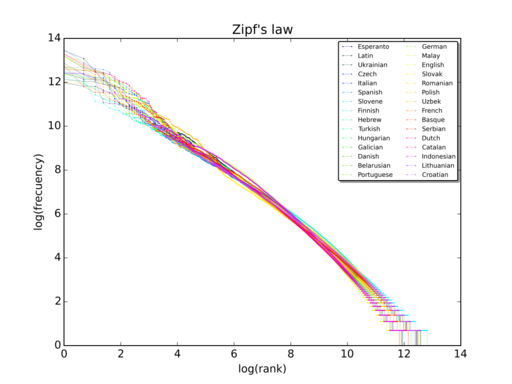
When s = 1, we don’t have a probability distribution because the sum of 1/n from 1 to ∞ diverges. And so no, we cannot assume N = ∞.
Now you may object that all we have to do is set s to be slightly larger than 1. If s = 1.0000001, then the sum of n−s converges. Problem solved. But not really.
When s = 1 the series diverges, but when s is slightly larger than 1 the sum is very large. Practically speaking this assigns too much probability to rare words.
If s = 2, for example, one could set N = ∞. The Zipf distribution with s = 2 may be useful for modeling some things, but not for modeling word frequency.
Zipf’s law applied to word frequency is an interesting example of a model that contains a large N, and although it doesn’t matter exactly how large N is, it matters that N is finite. In the earlier article, I used the estimate that Chinese has 50,000 characters. If I had estimated 60,000 characters the conclusion of the article would not have been too different. But assuming an infinite number of characters would result in substantially overestimating the frequency of rare words.
Related posts
Image above by Sergio Jimenez, CC BY-SA 4.0, via Wikimedia Commons

In high-energy physics ‘big and indeterminate, but certainly not infinite’ is a very common kind of number. The corresponding intuition to bridge the two cases s=1 would be to introduce a cutoff: work with a Zipf’s law density multiplied by a (possibly smoothed) indicator function [n<N] for some large N, and then look at the dependency on N in order to characterize and possibly correct the 'infrared' behaviour of the model.