Ancient estimate of π and modern numerical analysis

A very crude way to estimate π would be to find the perimeter of squares inside and outside a unit circle.

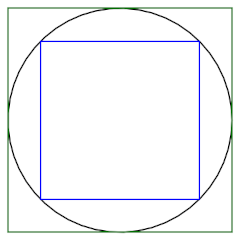
The outside square has sides of length 2, so 2π < 8. The inside square has sides of length 2/√2, so 8/√2 < 2π. This tells us π is between 2.82 and 4. Not exciting, but it’s a start.

Finding the perimeter of an inscribed hexagon and a circumscribed hexagon would be better. Finding the perimeter of inscribed and circumscribed n-gons for larger values of n would be even better.

Archimedes and successors

Archimedes (287–212 BC) estimated π using inscribed and circumscribed 96-gons.

Aryabhata (476–450 AD) used Archimedes idea with n = 384 (3 × 2⁷) and Vièta (1540–1603) used n = 39,3216 (3 × 2¹⁷).

Accuracy

The perimeter of a regular n-gon inscribed in the unit circle is

T_n = 2n sin(π/n)

and the perimeter of a regular n-gon circumscribed on the unit circle is

U_n = 2n tan(π/n).

We look at these formulas and see a way to calculate T_n and U_n by plugging π/n into functions that calculate sine and cosine. But Archimedes et al had geometric ways of computing T_n and U_n and used these to estimate π.

We can use the formulas above to evaluate the bounds above.

Archimedes: 3.1410 < π < 3.1427.

Aryabhata: 3.14155 < π < 3.14166.

Vièta: 3.14159265355 < π < 3.1415926536566.

Extrapolation

In 1654, Huygens discovered that algebraic combinations of the perimeter estimates for an n-gon and an (n/2)-gon could be better than either. So, for example, while Archimedes estimate based on a 96-gon is better than an estimate based on a 48-gon, you could combine the two to do better than both.

His series were

S_n = (4T_n − T_n/2)/3

and

V_n = (2U_n + T_n/2)/3

Huygens did not prove that S_n and V_n were lower and upper bounds on 2π, but they are, and are much better than T_n and U_n. Using a 48-gon and a 96-gon, for example, Huygens could get twice as many correct digits as Archimedes did with a 96-gon alone.

From a modern perspective, Huygens’ expressions can be seen as a first step toward what Richardson called “the deferred approach to the limit” in 1927, or what is often called Richardson extrapolation. By expanding the expressions for T_n and U_n as Taylor series in h = 1/n, we can take algebraic combinations of expressions for varying values of h that eliminate small powers of h, increasing the order of the approximation.

Huygens came up with expressions that canceled out terms of order h² and leaving terms of order h⁴. (The odd-order terms were already missing from sin(h)/h and tan(h)/h.)

Milne (1896–1950) came up with a systematic approach that could, for example, use polygons with n, n/2, and n/4 sides to come up with an approximation for π with order h⁶ and to form approximation with order equal to any even power of h. By making clever use of perimeter values known to Archimedes, Milne could obtain more accurate results than those that Aryabhata and Vièta obtained.

Richardson saw a general pattern in the work of Milne and others. We take expressions involving limits as h goes to 0, i.e. derivatives, and to do some manipulation before letting some h go to 0. Taking the derivative would be to take a limit immediately. But if we let some terms cancel each other out before taking the limit, we can get approximations that converge more quickly.

Richardson developed this idea used it as a way to solve a variety of problems more efficiently, such as numerical integration and numerically solving differential equations.

References

[2] D. C. Joyce. Survey of Extrapolation Process in Numerical Analysis by SIAM Review , Oct., 1971, Vol. 13, No. 4, pp. 435–490