I just saw a tweet from Dave Richeson saying
I remember as a kid calculating the size difference (diameter) of a belt between each hole. Now I think about it every time I wear a belt.
Holes 1 inch apart change the diameter by about one-third of an inch (1/π). [Assuming people have a circular waistline 🤣]
People do not have circular waistlines, unless they are obese, but the circular approximation is fine for reasons we’ll show below.
Robust approximations
Good simplifications, such as approximating a human waist by a circle, are robust. It doesn’t matter how well a circle approximates a waistline but rather how well the conclusion assuming a circular waistline approximates the conclusion for a real waistline.
There’s a joke that physicists say things like “assume a spherical cow.” Obviously cows are not spherical, but depending on the context, assuming a spherical cow may be a very sensible thing to do.
Elliptical waistlines
A human waistline may be closer to an ellipse than a circle. It’s not an ellipse either—it varies from person to person—but my point here is to show that using a different model results in a similar conclusion.
For a circle, the perimeter equals π times the diameter. So an increase of 1 inch in the diameter corresponds to an increase of 1/π in the perimeter, as Dave said.
Suppose we increase the perimeter of an ellipse by 1 and keep the aspect ratio of the ellipse the same. How much do the major and minor axes change?
The answer will depend on the aspect ratio of the ellipse. I’m going to guess that the aspect ratio is maybe 2 to 1. This corresponds to eccentricity e equal to 0.87.
The ratio of the perimeter of an ellipse to its major axis is 2E(p) where E is the complete elliptic integral of the second kind. (See, there’s a good reason Dave used a circle rather than an ellipse!)
For a circle, the eccentricity is 0, and E(0) = π/2, so the ratio of perimeter to the major axis (i.e. diameter) is π. For eccentricity 0.87 this ratio is 2.42. So a change in belt size of 1 inch would correspond to a change in major axis of 0.41 and a change in minor axis of 0.21.
Dave’s estimate of 1/3 of an inch the average of these two values. If you average the major and minor axes of an ellipse and call that the “diameter” then Dave’s circular model comes to about the same conclusion as our elliptical model, but avoids having to use elliptic integrals.
Perimeter to average axis ratio
The following graph shows the ratio of perimeter to average axis length for an ellipse. On the left end, aspect 1, we have a circle and the ratio is π. As the aspect ratio goes to infinity, the limiting value is 4.
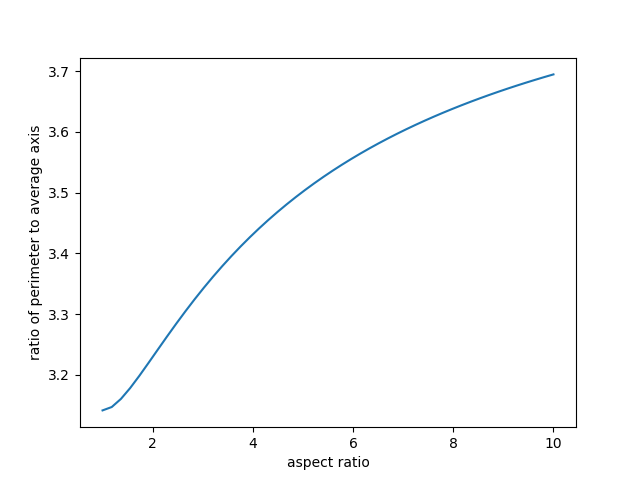
Even for substantial departures from a circle, such as a 2 : 1 or 3 : 1 aspect ratio, the ratio isn’t far from π.
