This post will compare the accuracy of approximations for the perimeter of an ellipse.
The exact perimeter is given in terms of an elliptic integral. (That’s where the elliptic integrals gets their name.) And so an obvious way to approximate the perimeter would be to expand the elliptic integral in a power series. Unfortunately this series converges slowly for highly eccentric ellipses.
Ernst Kummer found a series that converges more quickly [1]. Let a and b be the semi-major and semi-minor axes of an ellipse and let
Then Kummer’s series is
The following plot compares the accuracy of truncating Kummer’s series after powers of x equal to 1 through 4.
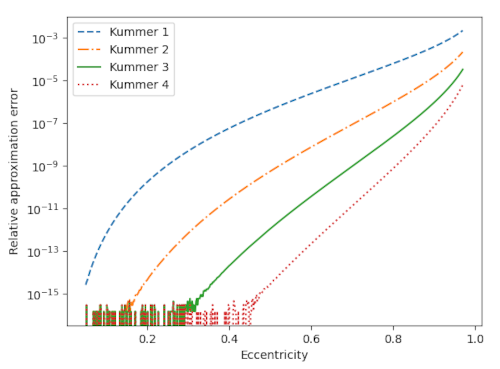
The noise at the bottom of the chart comes from the limits of machine precision. For moderate values of eccentricity, three terms of Kummer’s series gives an approximation so accurate that all the error is coming from the limitations of floating point resolution.
I’ve written about approximations for the perimeter of an ellipse before. The approximation based on the 3/2 norm is about as accurate as Kummer’s series truncated after the x term. The error in Ramanujan’s approximation is between that of Kummer’s series with the cubic and quartic terms.
For the orbit of Pluto (e = 0.2488) the first-order Kummer approximation is good to 9 figures and the higher-order approximations are essentially good to machine precision.
For the orbit of Haley’s comet (e = 0.9671) the successive Kummer approximations are good to 2, 3, 4, and 5 figures.
[1] Carl E. Linderholm and Arthur C. Segal. An Overlooked Series for the Elliptic Perimeter. Mathematics Magazine, Vol. 68, No. 3 (Jun., 1995), pp. 216–220.
