One year ago I wrote about a variant of the squircle that is quantitatively close to the customary definition but that has nicer algebraic properties.
That post used the term p-squircle for the usual squircle with equation
where p > 2, and the term s-squircle for the variation with equation
where s is between 0 and 1. When p = 2 or s = 0 we get a circle. As p goes to infinity or s = 1 we get a square.
Now the superegg is formed by rotating a squircle about an axis. To match the orientation in the posts I’ve written about supereggs, replace y with z above and rotate about the z-axis. We will also introduce a scaling factor h, dividing z by h.
The superegg analog of the s-squircle would have equation
The s-superegg is much easier to work with (for some tasks) than the p-superegg with equation
because the former is a polynomial equation and the latter is transcendental (unless p is an even integer). The s-superegg is an algebraic variety while the p-superegg is not in general.
Here’s a plot with s = 0.9 and h = 1.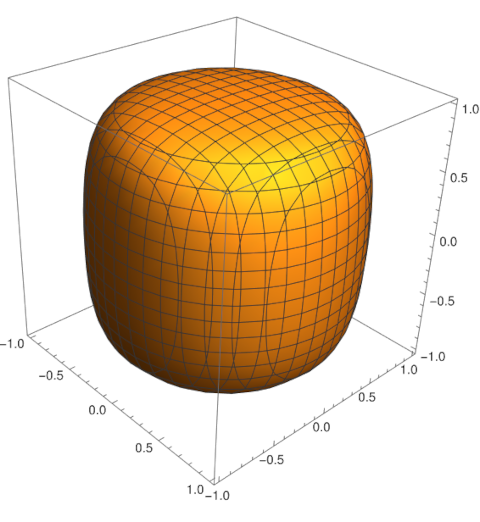
This plot was made with the following Mathematica code.
ContourPlot3D[
x^2 + y^2 + z^2 == 0.9^2 (x^2 + y^2) z^2 + 1,
{x, -1, 1}, {y, -1, 1}, {z, -1, 1}]
Yesterday I said that the p-superegg is stable for all p > 2 because the curvature at the bottom is 0. This means the center of curvature is at infinity, which is above the center of mass.
The s-superegg has positive curvature at the bottom for all 0 < s < 1 and so the center of curvature is finite. As s increases, the superegg becomes more like a cylinder and the center of curvature increases without bound. So the s-superegg will be stable for sufficiently large s.
I calculate the center of curvature in the next post.
