Something that seems like an isolated trick may turn out to be much more important. This is the case with a change of variables discovered by Karl Weierstrass.
Every calculus student learns a handful of standard techniques: u-substitutions, partial fractions, integration by parts, and trig substitutions. Then there is one more technique that is like something off a secret menu, something know only to the cognoscenti: Weierstrass’ t = tan(x/2) trick [1]. Michael Spivak called this “the world’s sneakiest substitution.”
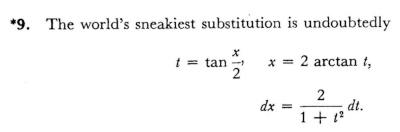
This was on page 325 of the first edition of Spivak’s Calculus, page 360 of the second edition.
This innocent but apparently unmotivated change of variables has the following magical consequences:
- sin(x) = 2t/(1 + t2)
- cos(x) = (1 – t2) / (1 + t2)
- dx = 2 dt/(1 + t2).
This means that the trick can convert an integral containing any rational combination of trig functions into one involving only rational functions, which then can (in principle) be integrated in closed form using partial fractions. It’s the key that unlocks all trig integrals.
However, this is not as practical as it sounds. You may get a high-degree rational function, and while in theory the rational function can be integrated using partial fractions, the decomposition may be tedious if not impossible. Still, it’s interesting that a single trick reduces one large class of integration problems to another.
Now let’s leave integration behind. The equations above say that as t varies, the functions 2t/(1 + t2) and (1 – t2) / (1 + t2) take on all the values that sin(x) and cos(x) do. This means, for example, that you can draw a circle using graphics hardware that does not support sines and cosines. In theory the range of t would have to be infinite, but in practice the range would only have to be large enough to fill in the right pixels.
If we can parameterize a circle with rational functions, what else can we parameterize this way? It turns out, for example, that elliptic curves do not have rational parameterizations. This question is its own niche of algebraic geometry. I don’t know the history here, but it’s plausible some of this math was motivated by wondering what else could be done along the lines of Weierstrass’ trick.
[1] When I’ve mentioned this trick before, some have told me this was a routine part of their course. That was not my experience, either as a student or as an instructor. As a freshman I learned the trick from a friend who was the best of our cohort at integration, someone who would have done well at an integration bee if we’d had one. I felt I’d been let in on a secret.