Logistic / Normal approximation

In a recent post I pointed out that a soliton, a solution to the KdV equation, looks a lot like a normal density for fixed x. As someone pointed out in the comments, one way to look at this is that the soliton is exactly proportional to the density of a logistic distribution, and it’s well known that the logistic distribution is approximately normal.

Why?

Why might this approximation be useful?

You might want to approximate a normal distribution by a logistic distribution because the cumulative density function of the latter is an elementary function whereas the CDF of the former is not.

You might want to approximate a logistic distribution by a normal distribution because the normal distribution has nice, well-understood theoretical properties.

How?

If you wanted to approximate a logistic distribution by a normal, or vice versa, how would you do so? How large is the error in the approximation?

This post will answer these questions for four matching methods:

1. Moment matching
2. 1-norm
3. 2-norm
4. Sup-norm

We will find the value of the logistic scale parameter s that minimizes the distance between the logistic PDF

f(x, s) = sech²(x / 2s) / 4s

and that of the standard normal

g(x) = (2π)^−1/2exp( − x²/2 )

by each of the criteria above. We set the scale parameter of the normal to 1 because the ratio of the optimal logistic scale to the normal scale is constant.

Moment matching

Let s be the scale parameter for the logistic distribution and let σ be the scale parameter for the normal distribution. We will assume both distributions have mean 0.

The variance of the logistic is π² s²/3 and the variance of the normal is σ². So moment matching requires

σ = π s / √3

or

s = √3 / π

since we’re setting σ = 1.

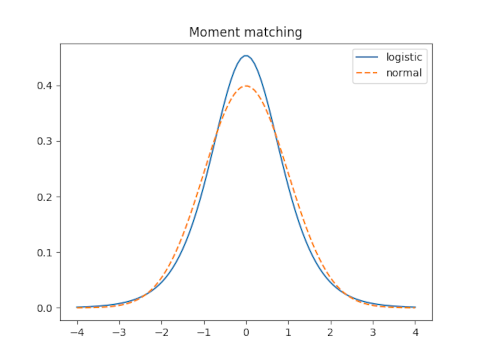
How good is this approximation? That depends on how you measure the error, which we will explore below. We will see how it compares to the optimal solution under each criterion.

1-norm

It would be nice to calculate the 1-norm of the difference f(x, s) − g(x) then minimize this as a function of s. But that difference cannot be computed in closed form. At least Mathematica can’t compute it in closed form. So I found the minimum numerically.

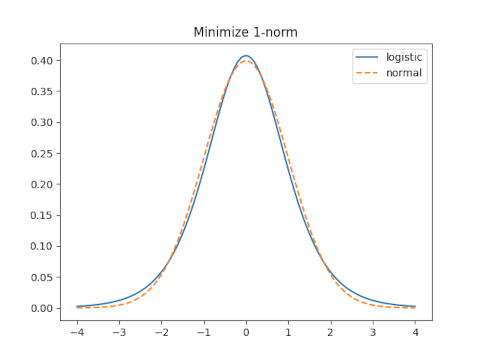
Moment matching sets s = 0.5513 and leads to a 1-norm error of 0.1087.

The optimal value of s for the 1-norm is s = 0.6137 which yields an error of 0.0665.

2-norm

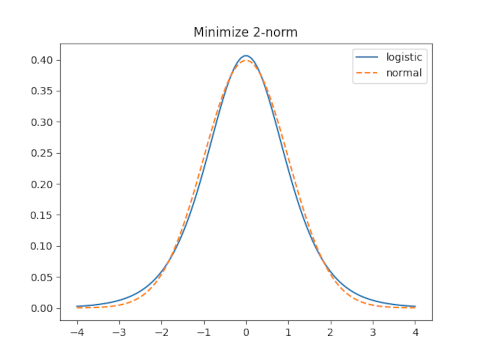
With moment matching s = 0.5513 and the 2-norm error is 0.05566.

The optimal value for the 2-norm is s = 0.61476 which yields a 2-norm error of 0.0006973.

sup-norm

The sup norm, a.k.a. min-max norm or ∞ norm, minimizes the maximum distance between the two functions.

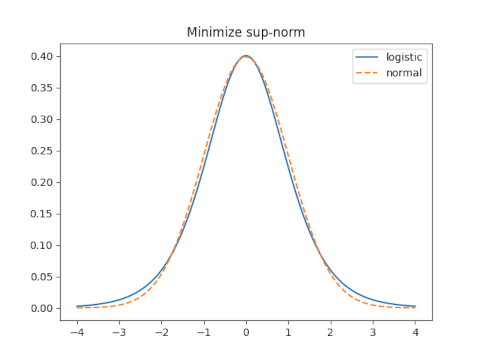
When s = 0.5513 the sup norm is 0.0545.

The optimal value of s for the sup norm is 0.6237 and yields a sup norm error of 0.01845.

Conclusion

We can improve on moment matching, for all three norms simultaneously, by using a larger value of s, such as 0.61.

If you have a normal(μ, σ) distribution and you want to approximate it by a logistic distribution, set the mean of the latter to μ and the scale to 0.61σ. If you care about a particular error measure, use the corresponding multiplier rather than 0.61.

If you want to approximate a logistic with mean μ and scale s by a normal, set the mean of the normal to μ and set σ = s/0.61.