Suppose you have a cable of length 2s suspended from two poles of equal height a distance 2x apart. Assuming the cable hangs in the shape of a catenary, how much does it sag in the middle?
If the cable were pulled perfectly taut, we would have s = x and there would be no sag. But in general, s > x and the cable is somewhat lower in the middle than on the two ends. The sag is the difference between the height at the end points and the height in the middle.
The equation of a catenary is
y = a cosh(t/a)
and the length of the catenary between t = −x and t = x is
2s = 2a sinh(x/a).
You could solve this equation for a and the sag will be
g = a cosh(x/a) − a.
Solving for a given s is not an insurmountable problem, but there is a simple approximation for g that has an error of less than 1%. This approximation, given in [1], is
g² = (s − x)(s + x/2).
To visualize the error, I set x = 1 and let a vary to produce the plot below.
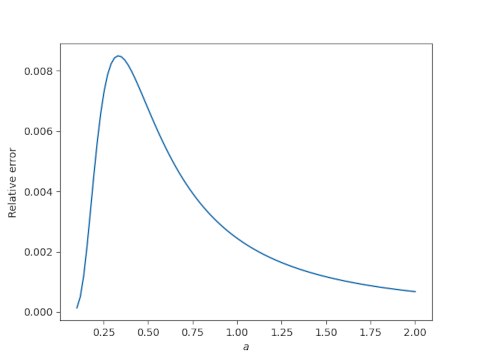
The relative error is always less than 1/117. It peaks somewhere around x = 1/3 and decreases from there, the error getting smaller as a increases (i.e. the cable is pulled tighter).
Related posts
[1] J. S. Frame. An approximation for the dip of a catenary. Pi Mu Epsilon Journal, Vol. 1, No. 2 (April 1950), pp. 44–46

This very problem arises when you adjust the height of permanent pickleball (or tennis) nets. I give the solution on my web site. This problem is quite counterintuitive as you only have to make the net a little longer (about 1/3″) to get a much larger (4″) sag.
This problem is especially important when powerlines heat up under load on hot days, then droop close to nearby vegetation, the very thing that has triggered multiple vast wildfires, especially in Southern California.
Predicting this droop based on material physics would seem to be a straightforward problem, yet it seems to be beyond the abilities of local utilities to triage and mitigate in advance.