I ran across a graphic yesterday made by taking a sequence of steps of the same length, turning left on the nth step if n is prime, and otherwise continuing in the same direction.
Here’s my recreation of the first 1000 steps:
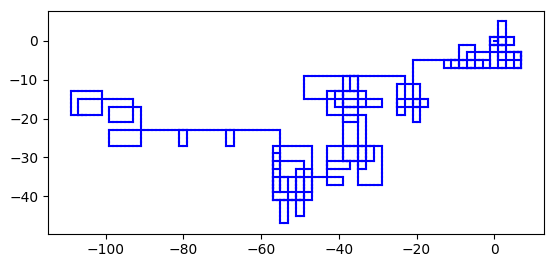
You can see that in general it makes a lot of turns at first and then turns less often as the density of primes thins out.
I wondered what the analogous walk would look like for Fizz Buzz. There are several variations on Fizz Buzz, and the one that produced the most interesting visualization was to turn left when a number either is divisible by 7 or contains the digit 7.
Here’s what that looks like:
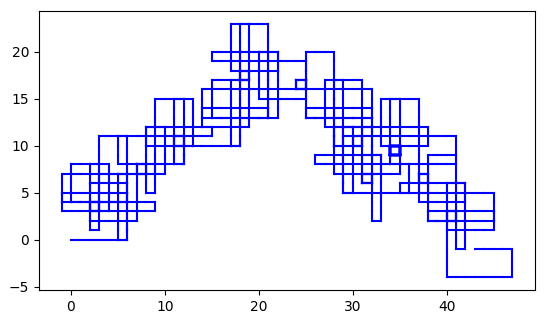
I wrote about something similar four years ago using a different rule for turning. That post looks at a walk on the complex numbers, turning left when you land on a Gaussian prime, a generalization of primes for complex numbers. These images have more symmetry and form closed loops. For example, here’s the walk you get starting at 3 + 5i.
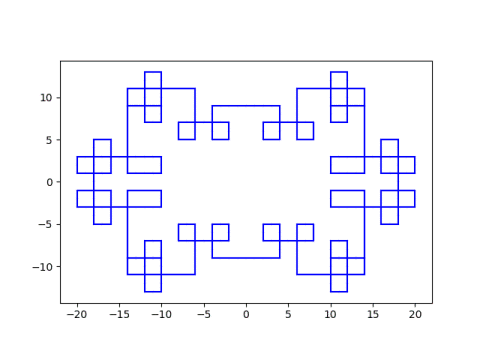
The starting point matters. See the earlier post for more examples with different starting points.
