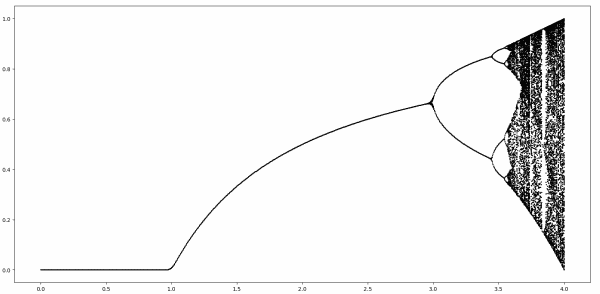
The previous post looked at iterations of the logistic map
f(x) = r x(1 − x)
for 0 ≤ r ≤ 3. This post will look at the range 3 ≤ r ≤ 1 + √6. If you’re not familiar with the logistic map I’d suggest reading the previous post first then coming back to this one.
The previous post looked at the flat part of the curve below, as well as the arc. This part will look at the first fork of the image, starting where the image first splits and before it splits again. That is, out of this image,
we’re going to zoom in on just this part:
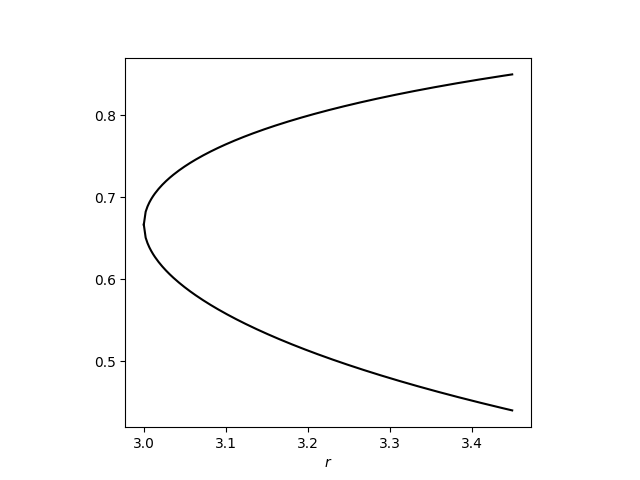
As before, x = (r − 1)/r is a fixed point. This was a stable fixed point for r < 3 but for r > 3 it is an unstable fixed point [1]. The image above shows stable fixed points. For r between 3 and 1 + √6 there is no stable fixed point, but there is a stable cycle.
The two branches are
Points near one point of the cycle are thrown to the other point.
Here’s a cobweb plot showing the iterations starting with x = 0.1 and r = π.
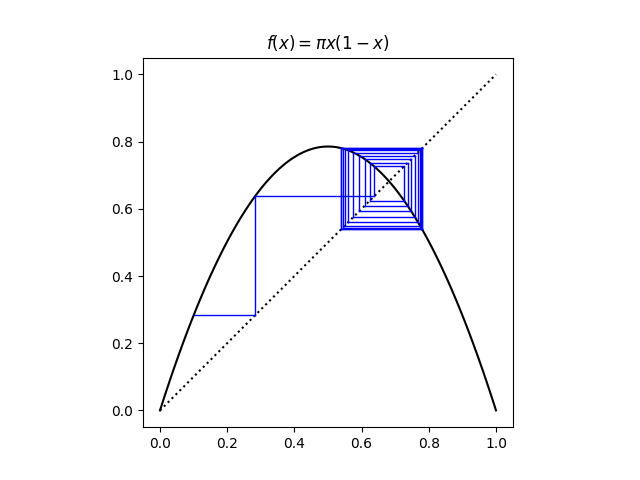
The dark blue box corresponds to the iterations converging to the two points of the cycle at 0.5373 and 0.7810. Here are the numerical values for the first 20 iterates.
0.2827
0.6371
0.7263
0.6245
0.7367
0.6093
0.7478
0.5924
0.7586
0.5754
0.7676
0.5605
0.7739
0.5497
0.7776
0.5432
0.7795
0.5399
0.7804
0.5384
If we apply the logistic map an even number of times, looking at iterations of f(f(x)), we get convergence to one branch or the other for almost all starting points. As you might expect from the previous post, convergence is slow for values of r at the beginning and end of the interval.
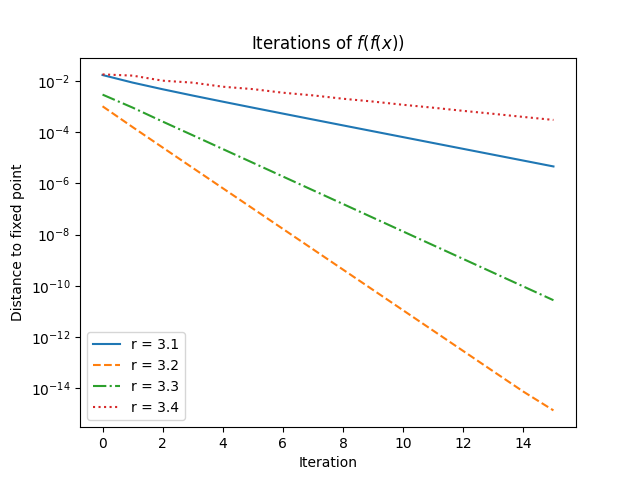
Note that the slowest convergence, the dotted line on top, corresponds to r = 3.4, close to 1 + √6 = 3.4495.
The slowest convergence comes from the values of r closest to the end points of the interval
[3, 1 + √6]
defining the first fork and the fastest convergence comes from the values of r in the middle of the interval.
Larger values of r
When r is larger than 1 + √6, the stable cycle points discussed above become unstable, and four new cycle points appear. This is called period doubling. We went from a cycle to a length 2 to a cycle of length 4. The number of periods keeps doubling as r increases, up to a point, around r = 3.56995. Beyond that point is literally chaos, i.e. chaos in the technical sense of the word.
Related posts
[1] A fixed point is stable if points near that point are drawn into that point. A fixed point is unstable if nearby points are repelled away from it.
