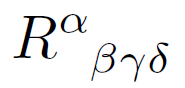I’ve started a new Twitter account: @tensor_fact.
The word “tensor” is used to describe several different but related mathematical objects. My intention, at least for now, it to focus on tensor calculus: things with indices that obey certain transformation rules.
More on other meanings of tensor here.
This morning I was working on a linear algebra problem for a client that I first solved by doing calculations with indices. As I was writing things up I thought of the phrase “the debauch of indices” that mathematicians sometimes use to describe tensor calculations. The idea is that calculations with lots of indices are inelegant and that more abstract arguments are better.
The term “debauch of indices” pejorative, but I’ve usually heard it used tongue-in-cheek. Although some people can be purists, going to great lengths to avoid index manipulation, pragmatic folk move up and down levels of abstraction as necessary to get their work done.
I searched on the term “debauch of indices” to find out who first said it, and found an answer on Stack Exchange that traces it back to Élie Cartan. Cartan said that although “le Calcul différentiel absolu du Ricci et Levi-Civita” (tensor calculus) is useful, “les débauches d’indices” could hide things that are easier to see geometrically.
After solving my problem using indices, I went back and came up with a more abstract solution. Both approaches were useful. The former cut through a complicated problem formulation and made things more tangible. The latter revealed some implicit pieces of the puzzle that needed to be made explicit.
This post will start with a motivating example, looking at measuring a room in inches and in feet. Then we will segue into a discussion of contravariance and covariance in the simplest setting. Then we will discuss contravariant and covariant tensors more generally.
In my previous post, I explained why it doesn’t matter if a tape measure is perfectly straight when measuring a long distance. In a nutshell, if you want to measure x, but instead you measure the hypotenuse of a triangle with sides x and y, where y is much smaller than x, the difference is approximately y²/2x. The error is nowhere as big as y.
In that post I gave the example of measuring a wall that is 10 feet long, and measuring to a point 4 inches up the adjacent wall rather than measuring to the corner. The error is about 1/15 of an inch.
Now suppose we’re off by more, measuring 12 inches up the other wall. Now that we have an even foot, we can switch over to feet and work with smaller, simpler numbers. Now we have x = 10 and y = 1. So the error is approximately 1/20.
Before, we were working in inches. We had x = 120, y = 4, and error 1/15. Does that mean our error is now smaller? That can’t be. If the short leg of our triangle is longer, 12 inches rather than 4 inches, our error should go up, not down.
Of course the resolution is that our error was 1/15 of an inch in the first example, and 1/20 of a foot in the second example. If we were to redo our second example in inches, we’d get error 12²/240 = 12/20, i.e. we’d convert 1/20 of a foot to 12/20 of an inch.
Now here’s where tensors come in. Notice that when we use a larger unit of measurement, a foot instead of an inch, we get a smaller numerical value for error. Trivial, right? If you first measure a distance in meters, you’ll get larger numbers if you switch to centimeters, but smaller numbers if you switch to light years.
But this simple observation is an example of a deeper pattern. Measurements of this kind are contravariant, meaning that our numerical values change in the opposite direction as our units of measurement.
A velocity vector is contravariant because if you use smaller units of length, you get larger numerical values of velocity, and vice versa. Under a change of units, velocity changes in the opposite direction of the units.
A gradient vector is covariant because if you use smaller units of length, a function will vary less per unit length. Gradients change in the same direction as your units.
The discussion so far has been informal and limited to a very special change of coordinates. It’s not just the direction of change that matters, that results change monotonically with units, but that they increase or decrease by the exact same proportion. And the kinds of coordinate changes we usually have in mind are not changing from inches to feet but rather changing from rectangular coordinates to polar coordinates.
Suppose you have some function T described by coordinates denoted by x‘s with superscripts. Put bars on top of everything to denote a new representation of T with respect to new coordinates. If T is a contravariant vector we have,
and if T is a covariant vector we have
In the equations above there is an implicit summation over the repeated index r, using the so-called Einstein summation convention.
The examples at the end of the previous section are the canonical examples: tangent vectors are contravariant and gradients are covariant.
If the xs without bars are measured in inches and the xs with bars are measured in feet, the partial derivative of an x bar with respect to the corresponding x is 1/12, because a unit change in inches causes a change of 1/12 in feet.
Vectors are a special case of tensors, called 1-tensors. Higher order tensors satisfy analogous rules. A 2-tensor is contravariant if
and covariant if
Even more generally you can have tensors of any order, and they can be contravariant in some components and covariant in others.
For more on tensors, you may want to read a five-part series of blog posts I wrote starting with What is a tensor?. The word “tensor” is used in several related but different ways. The view of tensors given here, as things that transform a certain way under changes of coordinates, is discussed in the fourth post in that series.
Sometimes simple notation can make a big difference. One example of this is the Kronecker delta function δij which is defined to be 1 if i = j and zero otherwise. Because branching logic is built into the symbol, it can keep branching logic outside of your calculation. That is, you don’t have to write “if … else …” in when doing your calculation. You let the symbol handle it.
The permutation symbol εijk is similar. It has some branching logic built into its definition, which keeps branching out of your calculation, letting you handle things more uniformly. In other words, the symbol encapsulates some complexity, keeping it out of your calculation. This is analogous to how you might reduce the complexity of a computer program. [1]
The permutation symbol, sometimes called the Levi-Civita symbol, can have any number of subscripts. If any two of the subscripts are equal, the symbol evaluates to 0. Otherwise, the symbol evaluates to 1 or -1. If you can order the indices with an even number of swaps, the sign of the permutation is 1. If it takes an odd number of swaps, the sign is -1. You could think of putting the indices into a bubble sort algorithm and counting whether the algorithm does an even or odd number of swaps.
(There’s an implicit theorem here saying that the definition above makes sense. You could change one order of indices to another by different series of swaps. Two different ways of getting from one arrangement to another may use a different number of swaps, but the number of swaps in both approaches will have the same parity.)
Incidentally, I mentioned even and odd permutations a few days ago in the context of finite simple groups. One of the families of finite simple groups are the alternating groups, the group of even permutations on a set with at least five elements. In other words, permutations whose permutation symbol is 1.
For example, ε213 = -1 because it takes one adjacent swap, exchanging the 2 and the 1, to put the indices in order. ε312 = 1 because you can put the indices in order with two adjacent swaps: 3 <-> 1, then 3 <-> 2. The symbol ε122 is 0 because the last two indices are equal.
You can compute permutation symbols in Mathematica with the function Signature. For example,
Signature[{3, 1, 2}]
returns 1. The function works with more indices as well. For example,
Signature[{3, 1, 2, 5, 4}]
returns -1.
SymPy has a function LeviCivita for computing the permutation symbol. It also has Eijk as an alias for LeviCivita. Both take a variable number of integers as arguments, not a list of integers as Mathematica does. If you do have a list of integers, you can use the * operator to unpack the list into separate arguments.
from sympy import Eijk, LeviCivita
from numpy.random import permutation
print( LeviCivita(3, 1, 2) )
print( Eijk(3, 1, 2, 5, 4) )
p = permutation(5)
assert(Eijk(*p) == LeviCivita(*p))
When all indices are distinct, the permutation symbol can be computed from a product. For two indices,
For three indices,
and in general
An example use of the permutation symbol is cross products. The ith component of the cross product of b × c is
Here we’re using tensor notation where components are indicated by superscripts rather than subscripts, and there’s an implied summation over repeated indices. So here we’re summing over j and k, each running from 1 to 3.
Similarly, the triple product of vectors a, b and c is
This is also the determinant of the matrix whose rows are the vectors a, b, and c. Determinants of larger matrices work the same way.
This post started out by talking about the more familiar Kronecker delta as an introduction to the permutation symbol. There is a nice relation between the two given below.
If we set r = i we get the special case
[1] One way of measuring the complexity of a computer program is the maximum number of logic branches in any function. If you have a moderately complex function, and you replace an if-then statement with a call to a small function that has an if-then statement, you’ve reduced the overall complexity. This is sort of what the delta and permutation functions do.
There are two uses of the word scalar, one from linear algebra and another from tensor calculus.
In linear algebra, vector spaces have a field of scalars. This is where the coefficients in linear combinations come from. For real vector spaces, the scalars are real numbers. For complex vector spaces, the scalars are complex numbers. For vector spaces over any field K, the elements of K are called scalars.
But there is a more restrictive use of scalar in tensor calculus. There a scalar is not just a number, but a number whose value does not depend on one’s choice of coordinates. For example, the temperature at some location is a scalar, but the first coordinate of a location depends on your choice of coordinate system. Temperature is a scalar, but x-coordinate is not. Scalars are numbers, but not all numbers are scalars.
The linear algebraic use of scalar is more common among mathematicians, the coordinate-invariant use among physicists. The two uses of scalar is a special case of the two uses of tensor described in the previous post. Linear algebra thinks of tensors simply as things that take in vectors and return numbers. The physics/tensor analysis view of tensors includes behavior under changes of coordinates. You can think of a scalar as a zeroth order tensor, one that behaves as simply as possible under a change of coordinates, i.e. doesn’t change at all.
In the first post in this series I mentioned several apparently unrelated things that are all called tensors, one of these being objects that behave a certain way under changes of coordinates. That’s what we’ll look at this time.
In the second post we said that a tensor is a multilinear functional. A k-tensor takes k vectors and returns a number, and it is linear in each argument if you hold the rest constant. We mentioned that this relates to the “box of numbers” idea of a tensor. You can describe how a k-tensor acts by writing out k nested sums. The terms in these sums are called the components of the tensor.
Tensors are usually defined in a way that has more structure. They vary from point to point in a space, and they do so in a way that in some sense is independent of the coordinates used to label these points. At each point you have a tensor in the sense of a multilinear functional, but the emphasis is usually on the changes of coordinates.
Tensors in the sense that we’re talking about here come in two flavors: covariant and contravariant. They also come in mixtures; more on that later.
We consider two coordinate systems, one denoted by x‘s and another by x‘s with bars on top. The components of a tensor in the x-bar coordinate system will also have bars on top. For a covariant tensor of order one, the components satisfy
First of all, coordinates are written with superscripts. So xr is the r coordinate, not x to the power r. Also, this uses Einstein summation notation: there is an implicit sum over repeated indexes, in this case of r.
The components of a contravariant tensor of order one satisfy similar but different equation:
The components of a covariant tensor are written with subscripts, and the components of a contravariant tensor with superscripts. In the equation for covariant components, the partial derivatives are with respect to the new coordinates, the x bars. In the equation for contravariant components, the partial derivatives are with respect to the original coordinates, the x‘s. Mnemonic: when the indexes go down (covariant tensors) the new coordinates go down (in the partial derivatives). When the indexes go up, the new coordinates go up.
For covariant tensors of order two, the change of coordinate formula is
Here there the summation convention says that there are two implicit sums, one over r and one over s.
The contravariant counter part says
In general you could have tensors that are a mixture of covariant and contravariant. A tensor with covariant order p and contravariant order q has p subscripts and q superscripts. The partial derivatives have x-bars on bottom corresponding to the covariant components and x-bars on top corresponding to contravariant components.
We initially said a tensor was a multilinear functional. A tensor of order k takes k vectors and returns a number. Now we’d like to refine that definition to take two kinds of vectors. A tensor with covariant order p and contravariant order q takes p contravariant vectors and q covariant vectors. In linear algebra terms, in stead of simply taking k elements of a vector space V, we say our tensor takes p vectors from the dual space V* and q vectors from V.
You may be familiar with the terms covariant and contravariant from category theory, or its application to object oriented programming. The terms are related. As Michael Spivak explains, “It’s very easy to remember which kind of vector field is covariant, and which is contravariant — it’s just the opposite of what it logically ought to be [from category theory].”
In the previous post, we defined the tensor product of two tensors, but you’ll often see tensor products of spaces. How are these tensor products defined?
For example, you may have seen tensor product splines. Suppose you have a function over a rectangle that you’d like to approximate by patching together polynomials so that the interpolation has the specified values at grid points, and the patches fit together smoothly. In one dimension, you do this by constructing splines. Then you can bootstrap your way from one dimension to two dimensions by using tensor product splines. A tensor product spline in x and y is a sum of terms consisting of a spline in x and a spline in y. Notice that a tensor product spline is not simply a product of two ordinary splines, but a sum of such products.
If X is the vector space of all splines in the x-direction and Y the space of all splines in the y-direction, the space of tensor product splines is the tensor product of the spaces X and Y. Suppose a set si, for i running from 1 to n, is a basis for X. Similarly, suppose tj, for j running from 1 to m, is a basis for Y. Then the products si tj form a basis for the tensor product X and Y, the tensor product splines over the rectangle. Notice that if X has dimension n and Y has dimension m then their tensor product has dimension nm. Notice that if we only allowed products of splines, not sums of products of splines, we’d get a much smaller space, one of dimension n+m.
We can use the same process to define the tensor product of any two vector spaces. A basis for the tensor product is all products of basis elements in one space and basis elements in the other. There’s a more general definition of tensor products that doesn’t involve bases sketched below.
You can also define tensor products of modules, a generalization of vector spaces. You could think of a module as a vector space where the scalars come from a ring instead of a field. Since rings are more general than fields, modules are more general than vector spaces.
The tensor product of two modules over a commutative ring is defined by taking the Cartesian product and moding out by the necessary relations to make things bilinear. (This description is very hand-wavy. A detailed presentation needs its own blog post or two.)
Tensor products of modules hold some surprises. For example, let m and n be two relatively prime integers. You can think of the integers mod m or n as a module over the integers. The tensor product of these modules is zero because you end up moding out by everything. This kind of collapse doesn’t happen over vector spaces.
The first two posts in this series:
I plan to leave the algebraic perspective aside for a while, though as I mentioned above there’s more to come back to.
Next I plan to write about the analytic/geometric view of tensors. Here we get into things like changes of coordinates and it looks at first as if a tensor is something completely different.
The simplest definition of a tensor is that it is a multilinear functional, i.e. a function that takes several vectors, returns a number, and is linear in each argument. Tensors over real vector spaces return real numbers, tensors over complex vector spaces return complex numbers, and you could work over other fields if you’d like.
A dot product is an example of a tensor. It takes two vectors and returns a number. And it’s linear in each argument. Suppose you have vectors u, v, and w, and a real number a. Then the dot product (u + v, w) equals (u, w) + (v, w) and (au, w) = a(u, w). This shows that dot product is linear in its first argument, and you can show similarly that it is linear in the second argument.
Determinants are also tensors. You can think of the determinant of an n by n matrix as a function of its n rows (or columns). This function is linear in each argument, so it is a tensor.
The introduction to this series mentioned the interpretation of tensors as a box of numbers: a matrix, a cube, etc. This is consistent with our definition because you can write a multilinear functional as a sum. For every vector that a tensor takes in, there is an index to sum over. A tensor taking n vectors as arguments can be written as n nested summations. You could think of the coefficients of this sum being spread out in space, each index corresponding to a dimension.
Tensor products are simple in this context as well. If you have a tensor S that takes m vectors at a time, and another tensor T that takes n vectors at a time, you can create a tensor that takes m + n vectors by sending the first m of them to S, the rest to T, and multiply the results. That’s the tensor product of S and T.
The discussion above makes tensors and tensor products still leaves a lot of questions unanswered. We haven’t considered the most general definition of tensor or tensor product. And we haven’t said anything about how tensors arise in application, what they have to do with geometry or changes of coordinate. I plan to address these issues in future posts. I also plan to write about other things in between posts on tensors.
Next post in series: Tensor products
The word “tensor” is shrouded in mystery. The same term is applied to many different things that don’t appear to have much in common with each other.
You might have heard that a tensor is a box of numbers. Just as a matrix is a rectangular collection of numbers, a tensor could be a cube of numbers or even some higher-dimensional set of numbers.
You might also have heard that a tensor is something that has upper and lower indices, such as the Riemann tensor above, things that have arcane manipulation rules such as “Einstein summation.”
Or you might have heard that a tensor is something that changes coordinates like a tensor. A tensor is as a tensor does. Something that behaves the right way under certain changes of variables is a tensor.
And then there’s things that aren’t called tensors, but they have tensor products. These seem simple enough in some cases—you think “I didn’t realize that has a name. So it’s called a tensor product. Good to know.” But then in other cases tensor products seem more elusive. If you look in an advanced algebra book hoping for a simple definition of a tensor product, you might be disappointed and feel like the book is being evasive or even poetic because it describes what a tensor product does rather than what it is. That is, the definition is behavioral rather than constructive.
What do all these different uses of the word “tensor” have to do with each other? Do they have anything to do with the TensorFlow machine learning library that Google released recently? That’s something I’d like to explore over a series of blog posts.