Learning is not the same as just gaining information. Sometimes learning means letting go of previously held beliefs. While this is true in life in general, my point here is to show how this holds true when using the mathematical definition of information.
The information content of a probability density function p(x) is given by
![]()
Suppose we have a Beta(2, 6) prior on the probability of success for a binary outcome.
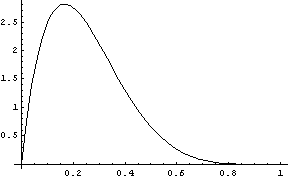
The prior density has information content 0.597. Then suppose we observe a success. The posterior density is distributed as Beta(3, 6). The posterior density has information 0.516, less information than the prior density.
Observing a success pulled the posterior density toward the right. The posterior density is a little more diffuse than the prior and so has lower information content. In that sense, we know less than before we observed the data! Actually, we’re less certain than we were before observing the data. But if the true probability of response is larger than our prior would indicate, we’re closer to the truth by becoming less confident of our prior belief, and we’ve learned something.
Related: Use information theory to clarify and quantify goals

Wouldn’t this problem be resolved if instead you calculated the differential relative (Kullback) entropy between the posterior and the prior? The posterior may be more dispersed than the prior but maybe the differential relative entropy (which is positive) reflects the situation after the observation better then the difference between the differential entropy of the posterior and the differential entropy of the prior (which as you observe is negative in this example).