Bayesian

Posterior variance

Posted on by John

A few days ago I wrote a post entitled Does additional data always reduce posterior variance?. In a nutshell, the answer is no, not always.

That led the previous post which looked at posterior means for three Bayesian models, showing how the posterior mean is a weighted average of the prior mean and the mean of the new data. The weights are precisions, which means something different for each model.

For the beta-binomial model, variance may increase when seeing unexpected data (details here), but precision always increases.

For the normal-normal model precision is the reciprocal of variance. Every new data point makes precision go up and posterior variance go down.

The Poisson-gamma model may be the most interesting. As stated in the previous post, if data has a Poisson distribution with parameter λ, and λ has a gamma(α0, β0) prior distribution, then the posterior distribution on λ after observing k events over time t has a gamma(α0 + k, β0 + t) posterior distribution. Therefore the posterior variance is

(α0 + k) / (β0 + t)².

Note the posterior variance is an increasing function of k and a decreasing function of t. This means that the posterior variance increases every time an event is observed, and it decreases quadratically between observations.

Here’s an illustration. I simulated data from a Poisson process with λ and used a gamma(1, 1) prior on λ. Here’s a plot of the posterior variance.

Posterior mean

Posted on by John

Common sense says that what you believe after seeing new data should be some sort of compromise between what you believed before and what the new data says. You don’t want to ignore previous information or new information.

How much should new data change your prior beliefs? When prior judgment and new information are in conflict, which one should be given the benefit of the doubt?

Bayesian data models provide a framework for making such decisions quantitative and objective. The choice of a data model is somewhat subjective—whether it’s a Bayesian model or not—but given a Bayesian model, the rules for updating the representation of your beliefs are objective. As some put it, you “turn the Bayesian crank.” A likelihood model and a prior on parameters together specify how new data changes the prior distribution into a posterior distribution.

We will make this more concrete with three examples.

Normal-normal model

Suppose that data X has a normal distribution with unknown mean μ and known variance σ², and we assume that a priori μ has a normal distribution with mean μ0 and variance σ0².

After observing x, the posterior distribution on μ also has a normal distribution, but with a different mean and variance. Its mean is somewhere between the prior mean and x. We will ignore the change in the variance for this post.

The posterior mean of μ is

\mu_{\text{post}} = \frac{\dfrac{\mu_0}{\sigma_0^2} + \dfrac{x}{\sigma^2}}{\dfrac{1}{\sigma_0^2} + \dfrac{1}{\sigma^2}}

This equation becomes more understandable when we introduce precisons τ = 1/σ² and τ0 = 1/σ0².

Then we have

\mu_{\text{post}} = \frac{\mu_0 \cdot \tau_0 + x \cdot \tau}{\tau_0 + \tau}

which you can read as saying the posterior mean is the weighted average of the prior mean and x, with the weights given by the precision. Intuitively, you take the weighted mean of your conclusions from previous data and new data, weighting the mean according to how much confidence you have in each.

Beta-binomial model

Now let’s switch over to a different data model. Now assume X is a binary random variable, with probability of success p and probability of failure 1 − p, and we assume p has a beta(a, b) distribution.

After observing s successes and f failures, the posterior mean of the distribution on p becomes

p_{\text{post}} = \frac{a + s}{a + b + s + f}

We can rewrite this as

p_{\text{post}} = \frac{(a + b) \dfrac{a}{a+b} + (s + f) \dfrac{s}{s+f}}{(a + b) + (s +f)}

This says that the posterior mean is the weighted average of the prior mean a/(a + b) and the mean of the data s/n. The weights are the prior effective sample size a + b and the sample size of the new data n. In this example (effective) sample size is playing the role that precision played in the normal-normal model above.

Gamma-Poisson model

Suppose data have a Poisson distribution with parameter λ, and λ has a gamma(α0, β0) prior distribution [1]. And suppose you observe k events over time t. Then the posterior distribution of λ given the data has a gamma(α0 + k, β0 + t) prior distribution and the mean of the posterior distribution is given by

\lambda_{\text{post}} = \frac{\alpha_0 + k}{\beta_0 + t} = \frac{\beta_0 (\alpha_0 / \beta_0) + t (k / t)}{\beta_0 + t}

As before, the posterior mean is a weighted average of the prior mean and new data, and the weights are interpretable as some sort of measure of confidence, namely time. The variable t is directly time and the parameter β0 is sort of an effective time, just as a + b is an effective sample size for the beta distribution.

Common thread

In each example the posterior mean is the weighted average of the prior mean and the mean of the data, with the weights given by a precision. However, precision means something different in each example. In the normal-normal model, precision is the reciprocal of variance, but in the beta-binomial model precision is sample size and in the Poisson-gamma model precision is time.

What all three examples have in common is that they are conjugate models using distributions from the “exponential family” of probability distributions. In technical terms, precision is the multiplicative factor on the sufficient statistic in the exponent of the posterior kernel.

Related posts

[1] There are multiple conventions for parameterizing the gamma distribution. Here we’re using the shape-rate parameterization, where the mean is α/β.

Does additional data always reduce posterior variance?

Posted on by John

A discussion over lunch today brought up the fact that additional data does not always decrease the size of a confidence interval. This post will look at this from a Bayesian perspective.

In general, new information reduces your uncertainty regarding whatever you’re estimating. The posterior distribution becomes more concentrated as more data are collected.

That’s what happens “in general” but does it necessarily happen every time you get new data? Conceivably if you get surprising data, data that is very unlikely given your current prior, posterior uncertainty might increase.

Beta-binomial model

To show that this is the case, suppose the probability of success in some binary trial has parameter θ and that θ has a beta prior. You could imagine this prior to be the posterior after having made some number of previous observations. Can a new observation increase the posterior variance in θ? If so, under what conditions?

The variance of a beta(a, b) random variable is

ab / (a + b)²(a + b + 1).

After observing a successful trial, the posterior distribution on θ is beta(a + 1, b). We can calculate the ratio of the posterior variance to the prior variance and ask under what circumstances, if any, the ratio is greater than 1.

If 2a ≥ b the posterior variance will be strictly less than the prior variance. This says if the prior mean odds against a success are no more than 2 : 1, observing a success will reduce the variance. (So will observing a failure.) But for any value of b, you can find a small enough value of a that observing a success will increase the variance.

Normal-normal model

Whether an observation can increase the posterior variance depends on the data model. If your data have a normal likelihood function with known variance and a normal prior on the mean θ, the posterior variance is always less than the prior observation, and it reduces by the same amount, independent of the observation x. If x is very unlikely a priori then it will pull the posterior mean toward itself more than an observation that is more concordant with the prior would have, but the change in the posterior variance is the same.

Proof of beta theorem

Here is a proof in Lean 4 of the statement above that if 2a ≥ b the posterior variance will be strictly less than the prior variance.

import Mathlib

set_option linter.style.header false

noncomputable def f (a b : ℝ) : ℝ := a * b / ((a + b) ^ 2 * (a + b + 1))

theorem f_ratio_lt_one' (a b : ℝ) (ha : 0 < a) (hb : 0 < b) (hab : b ≤ 2 * a) :
    f (a + 1) b / f a b < 1 := by
  have hs : 0 < a + b := by linarith
  have h2ab : 0 ≤ 2 * a - b := by linarith
  have hprod : 0 ≤ (a + b) * (2 * a - b) := mul_nonneg hs.le h2ab
  -- key polynomial inequality (∗)
  have key : (a + 1) * (a + b) ^ 2 < a * ((a + b + 1) * (a + b + 2)) := by
    nlinarith [hprod, ha]
  -- nonzero facts needed to clear denominators
  have ha' : a ≠ 0 := ne_of_gt ha
  have hb' : b ≠ 0 := ne_of_gt hb
  have hs' : a + b ≠ 0 := ne_of_gt hs
  have hs1' : a + b + 1 ≠ 0 := by positivity
  have hs2' : a + b + 2 ≠ 0 := by positivity
  have ha1' : a + 1 ≠ 0 := by positivity
  -- express the ratio as a single closed-form fraction
  have hratio : f (a + 1) b / f a b
      = ((a + 1) * (a + b) ^ 2) / (a * ((a + b + 1) * (a + b + 2))) := by
    unfold f
    have e : a + 1 + b = a + b + 1 := by ring
    rw [e]
    field_simp
    ring
  rw [hratio, div_lt_one (by positivity)]
  exact key

You can’t have everything you want: beta edition

Posted on by John

The beta distribution is a conjugate prior for a binomial likelihood function, so it makes posterior probability calculations trivial: you simply add your data to the distribution parameters. If you start with a beta(α, β) prior distribution on a proportion θ, then observe s successes and f failures, the posterior distribution on θ is

beta(α + s, β + f).

There’s an integration going on in the background, but you don’t have to think about it. If you used any other prior, you’d have to calculate an integral, and it wouldn’t have a simple closed form.

The sum α + β of the prior distribution parameters is interpreted as the number of observations contained in the prior. For example, a beta(0.5, 0.,5) prior is non-informative, having only as much information as one observation.

I was thinking about all this yesterday because I was working on a project where the client believes that a proportion θ is around 0.9. A reasonable choice of prior would be beta(0.9, 0.1). Such a distribution has mean 0.9 and is non-informative, and it would be fine for the use I had in mind.

Non-informative beta priors work well in practice, but they’re a little unsettling if you plot them. You’ll notice that the beta(0.9, 0.1) density has singularities at both ends of the interval [0, 1]. The singularity on the right end isn’t so bad, but it’s curious that a distribution designed to have mean 0.9 has infinite density at 0.

If you went further and used a completely non-informative, improper beta(0, 0) prior, you’d have strong singularities at both ends of the interval. And yet this isn’t a problem in practice. Statistical operations that are not expressed in Bayesian terms are often equivalent to a Bayesian analysis with an improper prior like this.

This raises two questions. Why must a non-informative prior put infinite density somewhere, and why is this not a problem?

Beta densities with small parameters have singularities because that’s just the limitation of the beta family. If you were using a strictly subjective Bayesian framework, you would have to say that such densities don’t match anyone’s subjective priors. But the beta distribution is very convenient to use, as explained at the top of this post, and so everyone makes a little ideological compromise.

As for why singular priors are not a problem, it boils down to the difference between density and mass. A beta(0.9, 0.1) distribution has infinite density at 0, but it doesn’t put much mass at 0. If you integrate the density over a small interval, you get a small probability. The singularity on the left is hard to see in the plot above, almost a vertical line that overlaps the vertical axis. So despite the curve going vertical, there isn’t much area under that part of the curve.

You can’t always get what you want. But sometimes you get what you need.

Related posts

The Rise and Fall of Bayesian Statistics

Posted on by John

At one time Bayesian statistics was not just a minority approach, it was considered controversial or fringe. When I was in grad school, someone confided in me that he was a closet Bayesian. He thought the Bayesian approach to statistics made sense, but didn’t want to jeopardize his career by saying so publicly.

Then somewhere along the way, maybe 20 years ago or so, Bayesian analysis not only became acceptable, it became hot. People would throw around the term Bayesian much like the throw around AI now.

During the Bayesian heyday, someone said that you’d know Bayes won when people would quit putting the word “Bayesian” in the title of their papers. That happened. I’m not sure when, but maybe around 2013? That was the year I went out on my own as a consultant. I thought maybe I could cash in on some of the hype over Bayesian statistics, but the hype had already subsided by then.

It’s strange that Bayes was ever scandalous, or that it was ever sexy. It’s just math [1]. You’d never look askance at someone for studying Banach algebras, nor would you treat them like a celebrity.

Bayesian statistics hasn’t fallen, but the hype around Bayesian statistics has fallen. The utility of Bayesian statistics has improved as the theory and its software tools have matured. In fact, it has matured to the point that people don’t emphasize that it’s Bayesian.

[1] Statistics isn’t exactly math, but that’s a topic for another day.

Condition on your data

Posted on by John

Suppose you design an experiment, an A/B test of two page designs, randomizing visitors to Design A or Design B. You planned to run the test for 800 visitors and you calculated some confidence level α for your experiment.

You decide to take a peek at the data after only 300 randomizations, even though your statistician warned you in no uncertain terms not to do that. Something about alpha spending.

You can’t unsee what you’ve seen. Now what?

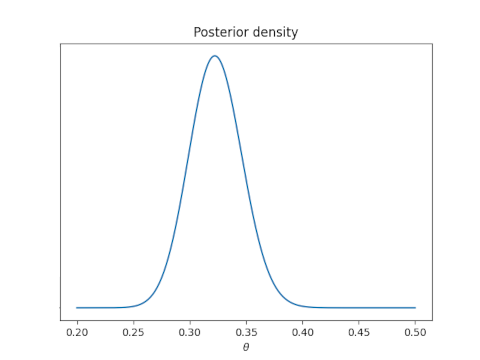
Common sense says it matters what you saw. If 148 people were randomized to Design A, and every single one of them bought your product, while 10 out of the 152 people randomized to Design B bought your product, common sense says you should call Design A the winner and push it into production ASAP.

But what if you saw somewhat better results for Design A? You can have some confidence that Design A is better, though not as much as the nominal confidence level of the full experiment. This is what your (frequentist) statistician was trying to protect you from.

When your statistician designed your experiment, he obviously didn’t know what data you’d see, so he designed a process that would be reliable in a certain sense. When you looked at the data early, you violated the process, and so now your actual practice no longer has the probability of success initially calculated.

But you don’t care about the process; you want to know whether to deploy Design A or Design B. And you saw the data that you saw. Particularly in the case where the results were lopsidedly in favor of Design A, your gut tells you that you know what to do next. You might reasonably say “I get what you’re saying about repeated experiments and all that. (OK, not really, but let’s say I do.) But look what happened? Design A is a runaway success!”

In formal terms, your common sense is telling you to condition on the observed data. If you’ve never studied Bayesian statistics you may not know exactly what that means and how to calculate it, but it’s intuitively what you’ve done. You’re making a decision based on what you actually saw, not on the basis of a hypothetical sequence of experiments you didn’t run and won’t run.

Bayesian statistics does formally what your intuition does informally. This is important because even though your intuition is a good guide in extreme cases, it can go wrong when things are less obvious. As I wrote about recently, smart people can get probability very wrong, even when their intuition is correct in some instances.

If you’d like help designing experiments or understanding their results, we can help.

Can you look at experimental results along the way or not?

Posted on by John

A B testing

Suppose you’re running an A/B test to determine whether a web page produces more sales with one graphic versus another. You plan to randomly assign image A or B to 1,000 visitors to the page, but after only randomizing 500 visitors you want to look at the data. Is this OK or not?

Of course there’s nothing morally or legally wrong with looking at interim data, but is there anything statistically wrong? That depends on what you do with your observation.

There are basically two statistical camps, Frequentist and Bayesian. (There are others, but these two account for the lion’s share.) Frequentists say no, you should not look at interim data, unless you apply something called alpha spending. Bayesians, on the other hand, say go ahead. Why shouldn’t you look at your data? I remember one Bayesian colleague mocking alpha spending as being embarrassing.

So who is right, the Frequentists or the Bayesians? Both are right, given their respective criteria.

If you want to achieve success, as defined by Frequentists, you have to play by Frequentist rules, alpha spending and all. Suppose you design a hypothesis test to have a confidence level α, and you look at the data midway through an experiment. If the results are conclusive at the midpoint, you stop early. This procedure does not have a confidence level α. You would have to require stronger evidence for early stopping, as specified by alpha spending.

The Bayesian interprets the data differently. This approach says to quantify what is believed before conducting the experiment in the form of a prior probability distribution. Then after each data point comes in, you update your prior distribution using Bayes’ theorem to produce a posterior distribution, which becomes your new prior distribution. That’s it. At every point along the way, this distribution captures all that is known about what you’re testing. Your planned sample size is irrelevant, and the fact that you’ve looked at your data is irrelevant.

Now regarding your A/B test, why are you looking at the data early? If it’s simply out of curiosity, and cannot affect your actions, then it doesn’t matter. But if you act on your observation, you change the Frequentist operating characteristics of your experiment.

Stepping back a little, why are you conducting your test in the first place? If you want to make the correct decision with probability 1 − α in an infinite sequence of experiments, then you need to take into account alpha spending, or else you will lower that probability.

But if you don’t care about a hypothetical infinite sequence of experiments, you may find the Bayesian approach more intuitive. What do you know right at this point in the experiment? It’s all encapsulated in the posterior distribution.

Suppose your experiment size is a substantial portion of your potential visitors. You want to experiment with graphics, yes, but you also want to make money along the way. You’re ultimately concerned with profit, not publishing a scientific paper on your results. Then you could use a Bayesian approach to maximize your expected profit. This leads to things like “bandits,” so called by analogy to slot machines (“one-armed bandits”).

If you want to keep things simple, and if the experiment size is negligible relative to your expected number of visitors, just design your experiment according to Frequentist principles and don’t look at your data early.

But if you have good business reasons to want to look at the data early, not simply to satisfy curiosity, then you should probably interpret the interim data from a Bayesian perspective. As the next post explains, the Bayesian approach aligns well with common sense.

I’d recommend taking either a Frequentist approach or a Bayesian approach, but not complicating things by hybrid approaches such as alpha spending or designing Bayesian experiments to have desired Frequentist operating characteristics. The middle ground is more complicated and prone to subtle mistakes, though we can help you navigate this middle ground if you need to.

If you need help designing, conducting, or interpreting experiments, we can help. If you want/need to look at interim results, we can show you how to do it the right way.

LET’S TALK

Related posts

A Bayesian approach to proving you’re human

Posted on by John

I set up a GitHub account for a new employee this morning and spent a ridiculous amount of time proving that I’m human.

The captcha was to listen to three audio clips at a time and say which one contains bird sounds. This is a really clever test, because humans can tell the difference between real bird sounds and synthesized bird-like sounds. And we’re generally good at recognizing bird sounds even against a background of competing sounds. But some of these were ambiguous, and I had real birds chirping outside my window while I was doing the captcha.

You have to do 20 of these tests, and apparently you have to get all 20 right. I didn’t. So I tried again. On the last test I accidentally clicked the start-over button rather than the submit button. I wasn’t willing to listen to another 20 triples of audio clips, so I switched over to the visual captcha tests.

These kinds of tests could be made less annoying and more secure by using a Bayesian approach.

Suppose someone solves 19 out of 20 puzzles correctly. You require 20 out of 20, so you have them start over. When you do, you’re throwing away information. You require 20 more puzzles, despite the fact that they only missed one. And if a bot had solved say 8 out of 20 puzzles, you’d let it pass if it passes the next 20.

If you wipe your memory after every round of 20 puzzles, and allow unlimited do-overs, then any sufficiently persistent entity will almost certainly pass eventually.

Bayesian statistics reflects common sense. After someone (or something) has correctly solved 19 out of 20 puzzles designed to be hard for machines to solve, your conviction that this entity is human is higher than if they/it had solved 8 out of 20 correctly. You don’t need as much additional evidence in the first case as in the latter to be sufficiently convinced.

Here’s how a Bayesian captcha could work. You start out with some distribution on your probability θ that an entity is human, say a uniform distribution. You present a sequence of puzzles, recalculating your posterior distribution after each puzzle, until the posterior probability that this entity is human crosses some upper threshold, say 0.95, or some lower threshold, say 0.50. If the upper threshold is crossed, you decide the entity is likely human. If the lower threshold is crossed, you decide the entity is likely not human.

If solving 20 out of 20 puzzles correctly crosses your threshold of human detection, then after solving 19 out 20 correctly your posterior probability of humanity is close to the upper threshold and would only require a few more puzzles. And if an entity solved 8 out of 20 puzzles correctly, that may cross your lower threshold. If not, maybe only a few more puzzles would be necessary to reject the entity as non-human.

When I worked at MD Anderson Cancer Center we applied this approach to adaptive clinical trials. A clinical trial might stop early because of particularly good results or particularly bad results. Clinical trials are expensive, both in terms of human costs and financial costs. Rejecting poor treatments quickly, and sending promising treatments on to the next stage quickly, is both humane and economical.

Related posts

Beta approximation to binomial

Posted on by John

It is well-known that you can approximate a binomial distribution with a normal distribution. Of course there are a few provisos …

Robin Williams imitating William F. Buckley

It is also well-known that you can approximate a beta distribution with a normal distribution as well.

This means you could directly approximate a binomial distribution with a beta distribution. This is a trivial consequence of the two other approximation results, but I don’t recall seeing this mentioned anywhere.

Why would you want to approximate a binomial distribution with a beta? The normal distribution is better known than the beta, and the normal approximation is motivated by the central limit theorem. However, approximating a binomial distribution by a beta makes the connection to Bayesian statistics clearer.

Let’s look back at a post I wrote yesterday. There I argued that the common interpretation of a confidence interval, while unjustified by the theory that produced it, could be justified by appealing to Bayesian statistics because a frequentist confidence interval, in practice, is approximately a Bayesian credible interval.

In that post I give an example of estimating a proportion p based on a survey with 127 positive responses out of 400 persons surveyed. The confidence interval given in that post implicitly used a normal approximation to a binomial. This is done so often that it typically goes unnoticed, and it is justified for large samples when p is not too close to 0 or 1.

Binomial distributions with large n are difficult to work with and it is more convenient to work with continuous distributions. Instead of the normal approximation, we could have used a beta approximation. This has nothing to do with Bayesian statistics yet. We could introduce the beta distribution simply as an alternative to the normal distribution.

The distribution on the estimated rate is binomial with p = 127/400 and variance p(1-p)/n with n = 400.

We could compare this to a beta distribution with the same mean and variance. I worked out here how to solve beta distribution parameters that lead to a specified mean and variance. If we do that with the mean and variance above we get a = 126.7 and b = 272.3. We could then find a 95% confidence interval by finding the 2.5 and 97.5 percentiles for a beta(126.7, 272.3) distribution. When we do, we get a confidence interval of (0.2728, 0.3639), very nearly what we got in the earlier post using a normal approximation.

At this point we have been doing frequentist statistics, using a beta distribution as a computational convenience. Now let’s put on our Bayesian hats. Starting with a uniform, i.e. beta(1, 1), prior, we get a posterior distribution on the proportion we’re estimating which has a beta(128, 274).

If you plot the density functions of a beta(126.7, 272.3) and a beta(128, 274) you’ll see that they agree to within the thickness of a line.

Related posts

Can you have confidence in a confidence interval?

Posted on by John

“The only use I know for a confidence interval is to have confidence in it.” — L. J. Savage

Can you have confidence in a confidence interval? In practice, yes. In theory, no.

If you have a 95% confidence interval for a parameter θ, can you be 95% sure that θ is in that interval? Sorta.

Frequentist theory

According to frequentist theory, parameters such as θ are fixed constants, though unknown. Probability statements about θ are forbidden. Here’s an interval I. What is the probability that θ is in I? Well, it’s 1 if θ is in the interval and 0 if it is not.

In theory, the probability associated with a confidence interval says something about the process used to create the interval, not about the parameter being estimated. Our θ is an immovable rock. Confidence intervals come and go, some containing θ and others not, but we cannot make probability statements about θ because θ is not a random variable.

Here’s an example of a perfectly valid and perfectly useless way to construct a 95% confidence interval. Take an icosahedron, draw an X on one face, and leave the other faces unmarked. Roll this 20-sided die, and if the X comes up on top, return the empty interval. Otherwise return the entire real line.

The resulting interval, either ø or (−∞, ∞), is a 95% confidence interval. The interval is the result of a process which will contain the parameter θ 95% of the time.

Now suppose I give you the empty set as my confidence interval. What is the probability now that θ is in the empty interval? Zero. What if I give you the real line as my confidence interval. What is the probability that θ is in the interval? One. The probability is either zero or one, but in no case is it 0.95. The probability that a given interval produced this way contains θ is never 95%. But before I hand you a particular result, the probability that the interval will be one that contains θ is 0.95.

Bayesian theory

Confidence intervals are better in practice than the example above. And importantly, frequentist confidence intervals are usually approximately Bayesian credible intervals.

In Bayesian statistics you can make probability statements about parameters. Once again θ is some unknown parameter. How might we express our uncertainty about the value of θ? Probability! Frequentist statistics represents some forms of uncertainty by probability but not others. Bayesian statistics uses probability to model all forms of uncertainty.

Example

Suppose I want to know what percentage of artists are left handed and I survey 400 artists. I find that 127 of artists surveyed were southpaws. A 95% confidence interval, using the most common approach rather than the pathological approach above, is given by

\left(\hat{p} - z_{1-\alpha/2} \sqrt{\frac{\hat{p}\hat{q}}{n}}, \hat{p} + z_{1-\alpha/2} \sqrt{\frac{\hat{p}\hat{q}}{n}} \right)

This results in a confidence interval of (0.272, 0.363).

Now suppose we redo our analysis using a Bayesian approach. Say we start with a uniform prior on θ. Then the posterior distribution on θ will have a beta(128, 264) distribution.

Now we can say in clear conscience that there is a 94% posterior probability that θ is in the interval (0.272, 0.363).

There are a couple predictable objections at this point. First, we didn’t get exactly 95%. No, we didn’t. But we got very close.

Second, the posterior probability depends on the prior probability. However, it doesn’t depend much on the prior. Suppose you said “I’m pretty sure most people are right handed, maybe 9 out of 10, so I’m going to start with a beta(1, 9) prior.” If so, you would compute the probability of θ being in the interval (0.272, 0.373) to be 0.948. Your a priori knowledge led you to have a little more confidence a posteriori.

Commentary

The way nearly everyone interprets a frequentist confidence interval is not justified by frequentist theory. And yet it can be justified by saying if you were to treat it as a Bayesian credible interval, you’d get nearly the same result.

You can often justify an informal understanding of frequentist statistics on Bayesian grounds. Note, however, that a Bayesian interpretation would not rescue the 95% confidence interval that returns either the empty set or the real line.

Often frequentist and Bayesian analyses reach approximately the same conclusions. A Bayesian can view frequentist techniques as convenient ways to produce approximately correct Bayesian results. And a frequentist can justify using a Bayesian procedure because the procedure has good frequentist properties.

There are times when frequentist and Bayesian results are incompatible, and in that case the Bayesian results typically make more sense in my opinion. But very often other considerations, such as model uncertainty, are much more substantial than the difference between a frequentist and Bayesian analysis.

Related posts