Here’s an image that came out of something I was working on this morning. I thought it might make an interesting border somewhere.
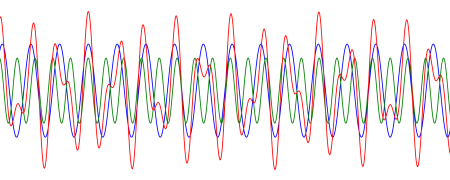
The blue line is sin(x), the green line 0.7 sin(φ x), and the red line is their sum. Here φ is the golden ratio (1 + √5)/2. Even though the blue and green curves are both periodic, their sum is not because the ratio of their frequencies is irrational. So you could make this image as long as you’d like and the red curve would never exactly repeat.
Update: See Almost periodic functions

Little known fact: If you play the red curve through speakers you will hear the voice of God
Very interesting although I can’t say the “border” appeals to me aesthetically.
A few other perhaps surprising facts about sums of periodic functions:
(a) The sum of two periodic functions can be a periodic function with a frequency higher than both constituents.
(b) It is possible to write the function f(x) = x as the sum of two periodic functions.
(c) It is impossible to write x² as the sum of two periodic functions.
@IJ (a) seems straight forward but (b) is blowing my mind a little. I assume the periodic functions aren’t continuous?
@Steven, that’s right. In fact, the functions are so strange you need the Axiom of Choice to assert their existence.
Do you have a reference? It seems to me any periodic function defined everywhere must be bounded, and the sum of two bounded functions must be bounded… What am I missing?
I don’t have a solid reference handy but take a look here:
http://cornellmath.wordpress.com/2008/01/22/periodic-functions-problem/
As far as I know, the fact that actual computers have finite precision implies that the ratio of the constituents frequency will be rational, given that each frequency will be a multiple of some negative power of two or ten. Therefore, their sum will in fact be periodic. Irrational numbers can only be represented symbolically in computers.
@I. J. Kennedy, what is it that means you can write f(x) = x as the sum of two periodic functions, but not f(x) = x²? Is it to do with x being uniformly continuous but x² not?
@John D. Cook, presumably the red line comes arbitrarily close to being periodic, in some sense, in the same way that rational combinations of 1 and sqrt(2) can come arbitrarily close to being rational?
I feel like I should be able to figure this out by myself, but just to confirm — when you say “the curve will never exactly repeat,” are you simply saying it’s not (globally) periodic, or that there exists no two non-empty intervals that match exactly?
The math is beyond me (as are most of the other comments here!) but I attempted to implement a SAS-language version of the squiggles. Thanks for the fun exercise — and let me know if I’ve got it wrong.
http://i1091.photobucket.com/albums/i395/mapperx/11SUNANDJDC01_zpsa0815d74.png
I DABBLE IN THE ART OF CONFORMAL MAPPING
AND USED YOUR SHIP IN SOME WORK.