Last week I wrote a blog post showing that powers of the golden ratio are nearly integers. Specifically, the distance from φn to the nearest integer decreases exponentially as n increases. Several people pointed out that the golden constant is a Pisot number, the general class of numbers whose powers are exponentially close to integers.
The so-called plastic constant P is another Pisot number, in fact the smallest Pisot number. P is the real root of x3 − x − 1 = 0.
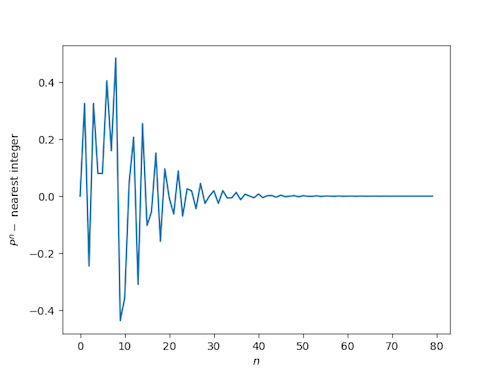
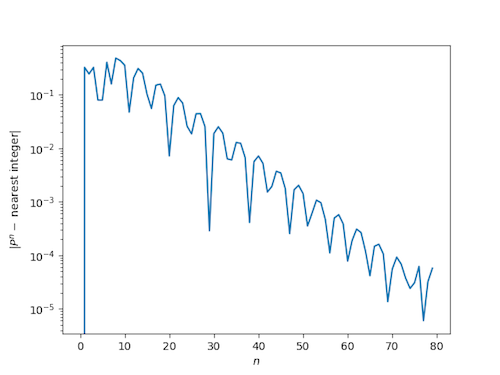
Because P is a Pisot number, we know that its powers will be close to integers, just like powers of the golden ratio, but the way they approach integers is more interesting. The convergence is slower and less regular.
We will the first few powers of P, first looking at the distance to the nearest integer on a linear scale, then looking at the absolute value of the distance on a logarithmic scale.
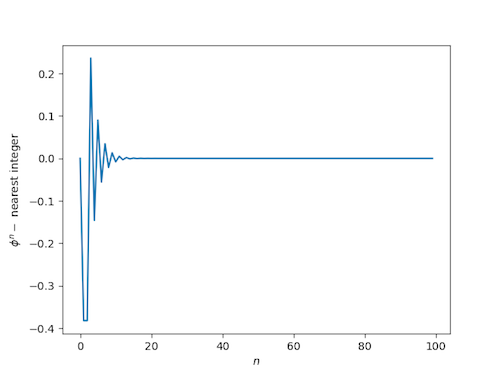
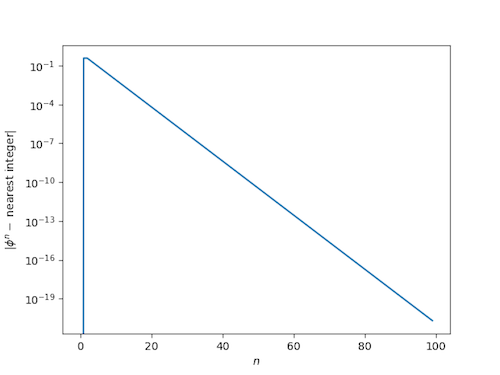
As a reminder, here’s what the corresponding plots looked like for the golden ratio.

Every nth Lucas number (2, 1, 3, 4, 7, …) is a sum of nth power of golden ratio and its negative nth power multiplied by (-1) to the nth. L(n) = Phi^n + phi^ (-n) . For instance: L(3) = 4 and adequately Phi^3 + phi^(-3) = 4. Consequently, with growing n value the second component the above sum vanishes and the first term asymptotically approaches the adequate Lucas number.
Regards,
PG13
BTW, the ratio of subsequent Lucas numbers L(n)/L(n-1) converges to the Golden Ratio.
Thought on phi, the Golden Ratio.
I once argued (in “Shtetl Optimized”) that phi turns up a lot because it is one of the 20 simplest (complex) algebraic numbers, as follows:
Assign a rank(x) to x as rank(x) = deg(x) + coefs(x), where
deg(x) = minimal degree as an algebraic number: 0 for integers, 1 for rational, 2 for square roots, etc.
coefs(x) = absolute sum of integer coefficients in minimal polynomial for x.
rank(x) = deg(x) + coefs(x)
In order of rank, with pm = plus or minus, and the total at the end:
rank = 2: 1x + 0 = 0; (1)
rank = 3: 1x + pm 1 = 0; (2)
rank = 4: 1x + pm 2 = 0; 2x +pm 1 = 0; 1x^2 + 0x +1 = 0 (5)
rank = 5: 1x + pm 3 = 0, 1x^2 + 0x + pm2 = 0; 3x + pm1 = 0, 1x^2 + 0x +pm 2 = 0, 1x^2 +pm 1x +pm 1 = 0 (12)
The last equation: x^2 – x – 1 = 0 gives phi. with a total of 20 numbers through rank 5.
Do you think this ranking for algebraic numbers is a useful idea?
Ralph
Here’s why the approach is more irregular:
Every one of these Pisot (or Pisot-Vijayaraghavan) numbers is the biggest root of some monic polynomial, that is, a polynomial with integer coefficients whose leading coefficient is 1. Every one of those polynomials corresponds to an integer recurrence sequence, and the integers are just the sums of powers of the roots of the polynomial: you raise all the roots to the nth power and add them together, and you get an integer.
For the golden ratio, the sequence is the Lucas numbers, and the other root is just -1/phi. Powers of phi approach integers smoothly because the difference is the powers of -1/phi.
For the plastic constant, the sequence is the Perrin numbers, and there are TWO other roots, which are complex conjugates. So the difference between powers of the plastic constant and Perrin numbers will be the sum of powers of those roots, which is a cosine function times a decaying exponential. So you’re seeing slightly more complicated oscillations.