When I first saw ring theory, my impression was that there were dozens of kinds of rings with dozens of special relations between them—more than I could keep up with. In reality, there just a few basic kinds of rings, and the relations between them are simple.
Here’s a diagram that shows the basic kinds of rings and the relations between them. (I’m only looking at commutative rings, and I assume ever ring has a multiplicative identity.)
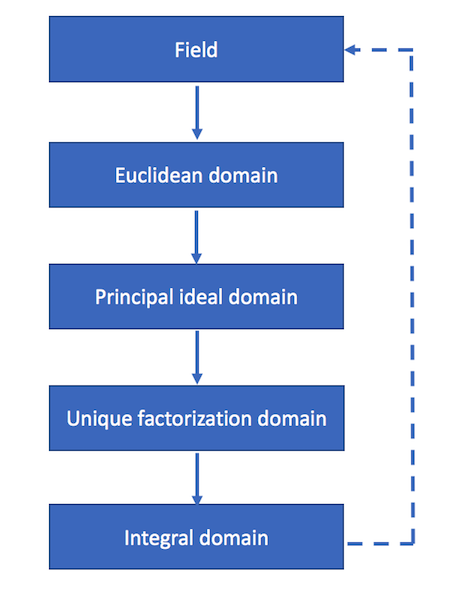
The solid lines are unconditional implications. The dashed line is a conditional implication.
- Every field is a Euclidean domain.
- Every Euclidean domain is a principal ideal domain (PID).
- Every principal ideal domain is a unique factorization domain (UFD).
- Every unique factorization domain is an integral domain.
- A finite integral domain is a field.
Incidentally, the diagram has a sort of embedded pun: the implications form a circle, i.e. a ring.
More mathematical diagrams:

Actually, the connections start being murky when you get to local rings, Noetherian rings, Dedekind rings, DVRs, Prufer rings and all that. At least, that is when I first got the impression that it can’t be possible to keep track of all the relations. When I first read your introduction, I thought you were going to provide a grand unified theory of that.
There is a Database of Ring Theory:
http://ringtheory.herokuapp.com
You can look up commutative rings that are unique factorization domain which are not principal ideal domain, for example.