Categorical data analysis could mean a couple different things. One is analyzing data that falls into unordered categories (e.g. red, green, and blue) rather than numerical values (e.g. height in centimeters).
Another is using category theory to assist with the analysis of data. Here “category” means something more sophisticated than a list of items you might choose from in a drop-down menu. Instead we’re talking about applied category theory.
So we have ((categorical data) analysis) and (categorical (data analysis)), i.e. analyzing categorical data and categorically analyzing data. The former is far, far more common.
I ran across Alan Agresti’s classic book the other day in a used book store. The image below if from the third (2012) edition. The book store had the 1st (1990) edition with a more austere cover.
I bought Agresti’s book because it’s a good reference to have. But I was a little disappointed. My first thought was that someone has written a book on category theory and statistics, which is not the case, as far as I know.
The main reference for category theory and statistics is Peter McCullagh’s 2002 paper What is a statistical model? That paper raised a lot of interesting ideas, but the statistics community did not take McCullagh’s bait.
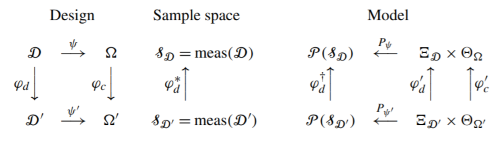
Maybe this just wasn’t a fruitful idea. I suspect it is a fruitful idea, but the number of people available to develop it, conversant in both statistics and category theory, is very small. I’ve seen category theory used in mathematical modeling more generally, but not in statistics per se.
At its most basic, category theory asks you to be explicit about the domain and range (codomain) of functions. It would be very helpful if statisticians merely did this. Statistical notation is notoriously bad at revealing where a function goes from and to, or even when a function is a function. Just 0th level category theory, defining categories, would be useful. Maybe it would be useful to go on to identifying limits or adjoints, but simply being explicit about “from” and “to” would be a good start.
Category theory is far too abstract to completely carry out a statistical analysis. But it can prompt you to ask questions that check whether your model has any inconsistencies you hadn’t noticed. The idea of a “categorical error” doesn’t differ that much moving from its philosophical meaning under Aristotle to its mathematical meaning under MacLane. Nor does the idea of something being “natural.” One of the primary motivations for creating category theory was to come up with a rigorous definition of what it means for something in math to be “natural.”


I think category theory is slowly making its way into data analysis, just not necessarily in the ways one might at first expect. The primary places I’ve seen category theory showing up is in deep learning (see Spivak and Fong’s “Backprop as Functor” for example, among others), and through the backdoor of topological data analysis. This is certainly not the categorical approach to statistics that you are discussing here, but I think it is an easier way to slip category theory in.
For my own part I am certainly interested in using category theory in data analytics and machine learning. I went to the trouble of designing an alternative to t-SNE (called UMAP) based on category theory and algebraic topology instead of probability theory. I think this approach makes for a more convincing argument for *why* such approaches work than t-SNE’s probability inspired description. I also believe I can use the same language and techniques to do clustering.
In summary — category theory is coming to data science, it is just taking the slow road via specific tools and techniques rather than trying to take over statistics.
The folks over at the n-category cafe occasionally touch on statistics and machine learning topics.
Really good blog,thank so much for your time in writing the posts.
I’ve wondered if there is an inkling of a category theory approach to statistics/approximation in the observation that an approximation of a sufficient statistic is a statistic with degraded sufficiency. A common situation in applied statistics is that your observations may be filtered through non-inventively functions and you may also only really be interested in components of the underlying variable that are most material to a domain-specific model.
I’m an actuary and studying mortality tables involves both of these issues. Relevant data may not be framed in the most efficient format for incorporating it into analysis and the precise shape of the table does not matter so much as coarse attributes like “level” and “slope”. Certain observations such as differences in “life expectancy” between two populations can be translated into approximately linear adjustments in “level” on a mortality table.
There are some different types of moving parts here but there is a notion that transformations on data are either invertible or degrade the data’s usefulness to reconstruct an underlying phenomenon and that we can also recast data based on its relevance to reconstruct aspects of the underlying phenomenon viewed as significant. The normal distribution is fully determined by the prior hypothesis that a data set’s only significant attributes are its mean and standard deviation and any other structure, real or imagined, of the data set can be discarded without consequences. Good statistics means systematically discarding irrelevant data (to the extent possible given the intractability of generalized statistical inference) and distilling relevant data. There are at least some operations that compose in this process.
You may want to check out Evan Patterson’s work, especially his Ph.D. thesis and associated talks:
https://www.epatters.org/papers/#2020-thesis
Thanks for letting me know about Evan Patterson.