There’s no perfectly satisfying way to map the globe on to a flat surface. Every projection has its advantages and disadvantages. The Mercator projection, for example, is much maligned for the way it distorts area, but it has the property that lines of constant bearing correspond to straight lines on the map. Obviously this is convenient if you’re sailing without GPS. But for contemporary use, say in a classroom, minimizing area distortion is often a higher priority than keeping bearing lines straight.
Bojan Šavrič, Tom Patterson, and Bernhard Jenny have developed a new map projection called Equal Earth that nicely balances several competing criteria, including aesthetics.
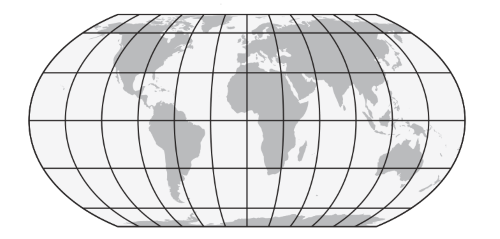
The Equal Earth projection satisfies the following mathematical criteria:
- Equal area: The area of a region on the globe is proportional to the area of its projection.
- Straight parallels: Lines of equal latitude project on to horizontal lines.
- Regularly distributed meridians: At a given latitude, the spacing between lines of longitude are equal.
- Bilateral symmetry: The projection is symmetric with respect to the x-axis (equator) and y-axis (prime meridian).
Here are the equations for the Equal Earth projection.
Here λ and φ are longitude and latitude respectively. The parametric latitude θ is introduced for convenience and is simply a rescaling of latitude φ.
The parameters ai are given below.
a_1 = 1.340264
a_2 = -0.081106
a_3 = 0.000893
a_4 = 0.003796
You can find more in their paper: Bojan Šavrič, Tom Patterson, and Bernhard Jenny. The Equal Earth map projection. International Journal of Geographical Information Science. https://doi.org/10.1080/13658816.2018.1504949.

I can’t find a source to purchase an Equal Earth Projection map.. To give my grand kids or to hang at home. Any ideas@