US Census area hierarchy

Posted on 11 November 2023 by John

Some kinds US Census geographic areas nest into a tidy hierarchy, but others do not. Here’s a brief overview of both.

Hierarchical entities

The orderly hierarchy is

nation
region
division
state
county
census tract
block group
census block.

All cleanly nested.

There are four regions: West, Midwest, Northeast, and South. Each region splits into two or three divisions. Each state falls within one division.

States are divided into counties, counties are divided into census tracts, census tracts are divided into block groups, block groups are divided into census blocks.

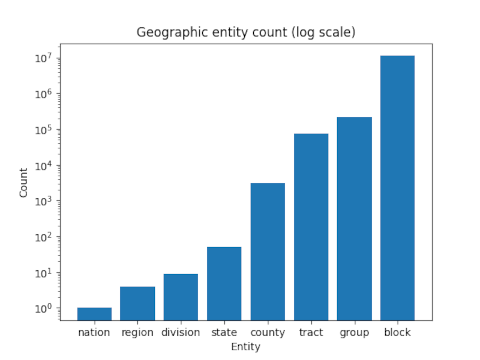
The number of entities at each level of the hierarchy is approximately geometrically increasing as show in the following log-scale bar graph. The number of entities at each level was based on the 2010 census.

1 nation, 4 regions, 9 divisions, 50 states, 3143 counties, 74134 tracts, 220742 block groups, 11166336 blocks

Organic entities

The Postal Service cares how mail delivery points are clustered and doesn’t care so much for legal and administrative borders. For this reason, zip codes represent mail delivery points and not geographic regions per se.

Zip codes are subject to change, and can straddle county or even state lines. Zip codes make sense from the US Postal Service, and they are their codes after all. But the temptation to use zip codes as geographic areas is so great that it is often done, even though it results in occasional strange behavior.

The US Census does not use zip codes per se, but rather Zip Code Tabulation Areas (ZCTAs), which basically correspond to zip codes, but rationalize them a bit from the perspective of geography.

Urban Areas and Core Based Statistical Areas (CBSAs) are based around cities, and since for practical purposes a city can spread across state lines, Urban Areas and CBSAs can cross state lines. The organic growth of a city may cross state lines, even if legally the city is divided into two cities.

Census blocks

Census blocks accommodate both the hierarchical and organic geographic areas. That is, a census block is contained entirely within a block group (which is contained within a census tract, which is contained within a county, …) but also within a single ZCTA and a single CBSA.

A disk around Paris

Posted on 1 November 2023 by John

The other day I saw an image of a large disk centered on Paris subjected to the Mercator projection. I was playing around in Mathematica and made similar images for different projections. Each image below is a disk of radius 4200 km centered on Paris (latitude 49°, longitude 2°).

All images were produced with the following Mathematica code, changing the GeoProjection argument each time.

    GeoGraphics[GeoDisk[GeoPosition[{49, 2}],
       Quantity[4200, "Kilometers"] ],
       GeoProjection -> "...", 
       GeoRange -> "World"]

Robinson projection

    … GeoProjection -> "Robinson", …

Robinson projection

Winkel-Snyder projection

    … GeoProjection -> "WinkelSnyder", …

Winkel-Snyder projection

Orthographic projection

    … GeoProjection -> "Orthographic", …

Orthographic projection

Lambert Azimuthal projection

    … GeoProjection -> "LambertAzimuthal", …

Lambert Azimuthal projection

Peirce Quincuncial projection

    … GeoProjection -> "PeirceQuincuncial", …

Peirce Quincuncial projection

This last projection has some interesting mathematics and history behind it. See this post for the backstory.

Creating a Traveling Salesman Tour of Texas with Mathematica

Posted on 10 August 2023 by John

A Traveling Salesman tour visits a list of destinations using the shortest path. There’s an obvious way to find the shortest path connecting N points: try all N! paths and see which one is shortest. Unfortunately, that might take a while.

Texas has 254 counties, and so calculating a tour of Texas counties by brute force would examine 254! paths, over 10⁵⁰⁰ paths. In theory, large Traveling Salesman problems are unsolvable. In practice they can often be solved quickly. As is often the case, the key is to give yourself just a little slack and look for solutions that are close to optimal.

I’ve used the example of a Traveling Salesman tour of Texas before because it makes a nice visual. People asked me for the code that made the image, but I didn’t save the code and didn’t remember offhand how to re-create it. So here’s the code for future reference.

Incidentally, computing the tour itself took only a second or two. Creating the visualization took several seconds.

    texas = Entity["AdministrativeDivision", "Texas"]; 
    counties = texas["Subdivisions"];
    tour = FindShortestTour[texas["Subdivisions"]];
    GeoGraphics[{Thick, Red, GeoPath[counties[[tour[[2]]]]]}]

Here counties is a list of objects representing Texas counties, sorted by alphabetical order, from Anderson County to Zavala County.

The tour object is a pair of a distance and a list of integers. The distance, 6780.74 nautical miles, is the length of the tour. The integers are the indexes of the counties in the tour.

{6780.74 nmi, {1, 107, 234, …, 201, 37, 1}}

The tour starts with the first county, Anderson County. It’s got to start somewhere, and I expect it always starts with the first item in the list. Next it goes to the 107th county, Henderson County, and so on. Because FindShortestTour returns a closed tour, the tour ends where it started, in Anderson County.

Related posts: Traveling Salesman tours of Africa, Americas, Eurasia and Oceania.

Mercator and polar projections

Posted on 13 November 2022 by John

This post is a more quantitative version of the previous post. Before I said that straight lines on a Mercator projection map correspond to loxodrome spirals on a sphere. This post will make that claim more explicit.

So suppose we plot a straight path from Quito to Jerusalem on a Mercator projection.

Quito to Jerusalem on a Mercator projection

The red dot in the lower left corner represents Quito and the next red dot represents Jerusalem.

Mercator projection leaves longitude λ unchanged, but latitude φ is transformed via

φ ↦ log( sec φ + tan φ )

for reasons explained here. We can apply the inverse of the Mercator projection to put the path above on a globe, and when we do, it looks like the following.

Loxodrome path from Quito to Jerusalem on a polar plot

The path planned on a Mercator projection map when projected onto the globe becomes a logarithmic spiral in polar projection. The radial direction in the plot above shows the angle down from the North Pole rather than the angle up from the equator.

So if our flight of constant bearing keeps going rather than stopping at Jerusalem, it will spiral quickly toward the North Pole. It appears to stop at pole unless you look carefully. In theory the spiral keeps going and never actually reaches the pole. This is easy to see on the Mercator map because the North Pole is infinitely far away on the vertical axis.

Straight on a map or straight on a globe?

Posted on 10 November 2022 by John

Straight lines on a globe are not straight on a map, and straight lines on a map are not straight on a globe.

A straight line on a globe is an arc of a great circle, the shortest path between two points. When projected onto a map, a straight path looks curved. Here’s an image I made for a post back in August.

Quito to Nairobi to Jerusalem and back to Quito

The red lines form a spherical triangle with vertices at Quito, Nairobi, and Jerusalem. The leg from Quito to Nairobi is straight because it follows the equator. And the leg from Nairobi to Jerusalem is straight because it follows a meridian. But the leg from Quito to Jerusalem looks wrong.

If you were flying from Quito to Jerusalem and saw this flight plan, you might ask “Why aren’t we flying straight there, cutting across Africa rather than making a big arc around it? Are we trying to avoid flying over the Sahara?”

But the path from Quito to Jerusalem is straight, on a globe. It’s just not straight on the map. The map is not the territory.

Now let’s look at things from the opposite direction. What do straight lines on a map look like on a globe? By map I mean a Mercator projection. You could take a map and draw a straight line from Quito to Jerusalem, and it would cross every meridian at the same angle. A pilot could fly from Quito to Jerusalem along such a path without ever changing bearing. But the plane would have to turn continuously to stay on such a bearing, because this is not a straight line.

A straight line on a Mercator projection is a spiral on a globe, known as a loxodrome or a rhumb line. If a plane flew on a constant bearing from Quito but few over Jerusalem and kept going, it would spiral toward the North Pole. It would keep circling the earth, crossing the meridian through Jerusalem over and over, each time at a higher latitude. On a polar projection map, the plane’s course would be approximately a logarithmic spiral. The next post goes into this in more detail.

loxodrome spiral

I made the image above using the Mathematica code found here.

Although straight lines the globe are surprising on a map, straight lines on a map are even more surprising on a globe.

Quirks in Mathematica’s administrative division data for Mexico

Posted on 5 October 2022 by John

If you ask Mathematica for a list of Mexican states via

    CountryData["Mexico", "RegionNames"]

you will get a list of strings:

    "Aguascalientes", "Baja California", ..., "Zacatecas"}

However, when you try to turn this into a list of objects representing these states via

    states = Entity["AdministrativeDivision", {#, "Mexico"}] & /@ 
                 CountryData["Mexico", "RegionNames"]

something strange happens. Some items in the list are turned into useful objects, and some are uninterpreted symbols.

For example, Aguascalientes is recognized as an administrative division, but Baja California is not. It recognizes Oaxaca but not Nuevo Leon. The pattern is that states with a space are not recognized. There is an inconsistency in Mathematica: output names do not always match input names. To create the object representing Baja California, you need to pass in the string BajaCalifornia with no space.

    Entity["AdministrativeDivision", {"BajaCalifornia", "Mexico"}]

OK, so let’s remove spaces before we try to create a list of geographic objects.

    names = StringReplace[#, " " -> ""] & /@ 
               CountryData["Mexico", "RegionNames"]

This mostly works, but it trips up on Mexico City. The output name for the region is Ciudad de México, but Mathematica does not recognize CiudaddeMéxico as an administrative division. Mathematica does recognize MexicoCity as the name of a city but not as the name of an administrative division.

Changing CiudaddeMéxico to MexicoCity in the list of names did not fix the problem. But when I directly edited the list of state objects by replacing the uninterpreted value with the output running

    Entity["AdministrativeDivision", {"MexicoCity", "Mexico"}]

by itself everything worked. Then I was able to find a Traveling Salesman tour as in earlier posts (Africa, Americas, Eurasia and Oceania, Canada).

Traveling Salesman tour of Mexico

The tour is

Baja California
Baja California Sur
Sinaloa
Durango
Zacatecas
Aguascalientes
Nayarit
Jalisco
Colima
Michoacán
México
Mexico City
Morelos
Guerrero
Oaxaca
Chiapas
Tabasco
Campeche
Quintana Roo
Yucatán
Veracruz
Puebla
Tlaxcala
Hidalgo
Querétaro
Guanajuato
San Luis Potosí
Tamaulipas
Nuevo León
Coahuila
Chihuahua
Sonora

The tour is 8,343 kilometers.

A traveling salesman tour of Canada

Posted on 4 October 2022 by John

Here is a Traveling Salesman tour of Canada’s provinces and territories created by Mathematica. This is the shortest path connecting the geographic centers of the regions.

Here is a much larger (4.5 MB) PDF file of the same map with higher resolution.

Starting in the northwest, the tour is

Yukon
Northwest Territories
Nunavut
Quebec
Newfoundland and Labrador
Prince Edward Island
Nova Scotia
New Brunswick
Ontario
Manitoba
Saskatchewan
Alberta
British Columbia

The tour is 11,070 km.

For more tours like this, see my earlier posts on tours of

Update: Here is an adjacency network for Canadian provinces and territories.

This is an SVG image so you can scale it to make it easier to read if you’d like.

Two-letter vs Three-letter Country Abbreviations

Posted on 19 September 2022 by John

The ISO 3166-1 standard defines three codes for each country: a 2-letter abbreviation, a 3-letter abbreviation, and a 3-digit code.

The 2-letter abbreviations may be familiar because it is very often (but not always [1]) also the country code top-level domain (ccTLD). For example, AU is the ISO abbreviation for Australia, and .au is the ccTLD.

I was curious about the relation between the two-letter and three-letter abbreviations. Sometimes the former is a prefix of the latter, such as US and USA. Sometimes the latter adds a letter in the middle, such as going from CN to CHN. How common are these two patterns?

I wrote a script using the iso3166 Python module to find out.

Turns out that the prefix pattern is most common, and occurs 63% of the time.

The infix pattern is the next most common, occurring 29% of the time.

Suffixes are rare. There are only for instances where the 2-letter name is the last two letters of the 3-letter name: ATF, MYT, SPM, and SGS.

The remaining possibilities are miscellaneous relations, such as IL and ISR for Israel.

Here’s a table of countries and ISO codes in plain text (org-mode) format.

[1] There are four ccTLDs that are not ISO 3166-1 alpha-2 names: uk, su, ac, and eu.

Finding similar world flags with Mathematica

Posted on 19 September 2022 by John

A week ago I posted some pairs of similar flags on Twitter, and later I found that Mathematica’s CountryData database contains flag descriptions. So I thought I’d use the flag descriptions to see which flags Mathematica things are similar.

For example, the FlagDescription attribute for Chad in Mathematica is

Three equal vertical bands of blue (hoist side), yellow, and red; similar to the flag of Romania; also similar to the flags of Andorra and Moldova, both of which have a national coat of arms centered in the yellow band; design was based on the flag of France.

I had Mathematica output a list of countries and flag descriptions, then searched the output for the word “similar.” I then made the following groupings based on the output [1].

Chad / Romania

Chad

Bolivia / Ghana

Bolivia Ghana

Colombia / Ecuador

Equador Columbia

India / Niger

India

Ireland / Côte d’Ivoire

Ireland Ivory Coast

El Salvador / Nicaragua / Honduras

El Salvador

Egypt / Iraq / Syria / Yemen

Iraq

Luxembourg / The Netherlands

Andorra / Moldova

Indonesia / Monaco

Indonesia Monaco

Emoji

Each flag has an emoji, so here are the groupings above using emoji icons

🇹🇩 🇷🇴
🇧🇴 🇬🇭
🇨🇴 🇪🇨
🇮🇳 🇳🇪
🇮🇪 🇨🇮
🇸🇻 🇳🇮 🇭🇳
🇪🇬 🇮🇶 🇸🇾 🇾🇪
🇱🇺 🇳🇱
🇦🇩 🇲🇩
🇮🇩 🇲🇨

[1] The groupings are based on Mathematica’s output, but I did some editing. Strictly following Mathematica’s descriptions would have been complicated. For example, Mathematica’s description might say A is similar to B, but not say B is similar to A. Or it might cluster four flags together that could better be split into two pairs.

Graphing Japanese Prefectures

Posted on 12 September 2022 by John

The two previous posts looked at adjacency networks. The first used examples of US states and Texas counties. The second post made suggestions for using these networks in a classroom. This post is a continuation of the previous post using examples from Japan.

Japan is divided into 8 regions and 47 prefectures. Here is a network diagram of the prefectures in the Kanto region showing which regions border each other. (In this post, “border” will be regions share a large enough border that I was able to see the border region on the map I was using. Some regions may share a very small border that I left out.)

This is a good example of why it is convenient in GraphViz to use variable names that are different from labels. I created my graphs using English versions of prefecture names, and checked my work using the English names. Then after debugging my work I changed the label names (but not the connectivity data) to use Japanese names.

To show what this looks like, my GraphViz started out like this

    graph G {
    layout=sfdp
    AI [label="Aichi"]
    AK [label="Akita"]
    AO [label="Aomori"]
    ...
    AO -- AK
    AO -- IW
    AK -- IW
    ...

and ended up like this

    graph G {
    layout=sfdp
    AI [label="愛知県"]
    AK [label="秋田県"]
    AO [label="青森県"]
    ...
    AO -- AK
    AO -- IW
    AK -- IW
    ...

Here’s a graph only showing which prefectures border each other within a region.

This image is an SVG, so you can rescale it without losing any resolution. Here’s the same image as a PDF.

Because this network is effectively several small networks, it would be easy to look at a map and figure out which nodes correspond to which prefectures. (It would be even easier if you could read the labels!)

Note that there are two islands—literal islands, as well as figurative islands in the image above—Hokkaido, which is its own region, and Okinawa, which a prefecture in the Kyushu region.

Here’s the graph with all bordering relations, including across regions.

The image above is also an SVG. And here’s the same image as a PDF.