How long does it take to find large primes?

Descriptions of cryptography algorithms often start with something like “Let p be a large prime” or maybe more specifically “Let p be a 256 bit prime.” How hard is it to find large prime numbers?

Let’s look at the question in base b, so we can address binary and base 10 at the same time. The prime number theorem says that for large n, the number of primes less than bⁿ is approximately

bⁿ / n log b

and so the probability that an n-digit number base b is prime is roughly 1 / n log b. If you select an odd b-digit number, you double your chances.

If you generate odd n-digit numbers at random, how long would it be until you find a prime? You might get lucky and find one on your first try. Or you might have extraordinarily bad luck and find a composite every time until you give up.

The number of tries until you find a prime is a geometric random variable with

p = 2 / n log b.

The expected value is 1 / p.

So, for example, if you wanted to find a 256-bit prime, you would need to test on average 256 log(2) / 2 = 89 candidates. And if you wanted to find a 100-digit prime, you’d need to test on average 100 log(10) / 2 = 115 candidates.

You could get more accurate bounds by using a refined variation of the prime number theorem. Also, we implicitly looked at the problem of finding a number with at most n digits rather than exactly n digits. Neither of these would make much difference to our final result. To back up this claim, let’s compare our estimate to a simulation that actually looks for primes.

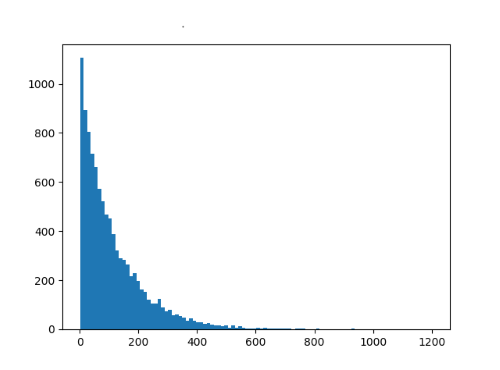
The histogram above was based on finding 10,000 primes, each with 100 digits, and counting how many candidates were evaluated each time. The plot matches a geometric distribution well. The mean from the simulation was 113.5, close to the 115 estimated above.

For cryptographic applications, you often don’t want just any prime. You might want a safe prime or a prime satisfying some other property, in which case you’ll need to test more primes. But your probability of success will likely still be geometrically distributed.

It’s plausible that for large p, p being prime and 2p + 1 being prime are independent events, at least approximately, and a numerical experiment suggests that’s true. I generated 10,000 primes, each 100-digits long, and 48 were safe primes, about what you’d expect from theory. It is not known whether the number of safe primes is infinite, but safe primes with hundreds of thousands of digits have been found, so apparently they’re infinite enough for application.

Related number theory posts

• Probability that a number is prime
• Elliptic curves over finite fields
• Schnorr groups