A recent video by Quanta Magazine says that the eigenvalues of random matrices and the zeros of the Riemann zeta function appear to have the same distribution.
I assume by “random matrices” the video is referring specifically to Gaussian orthogonal ensembles. [Update: See the first comment below for more details. You need some assumptions on the distribution—fat tails are out—but you don’t need to assume a GOE.]
By zeros of the Riemann zeta function, they mean the imaginary parts of the zeros in the critical strip. You can download the first 100,000 zeros of the Riemann zeta function here. So, for example, the first zero is 14.134725142, which actually means 0.5 + 14.134725142 i.
Here’s the histogram of random matrix eigenvalues from my previous post:
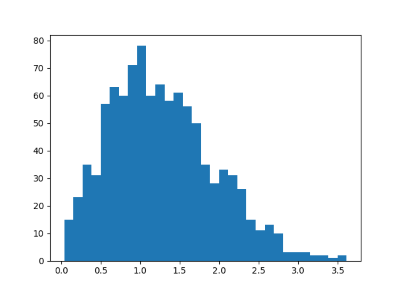
And here’s a histogram of the spacing between the first two thousand zeros of the Riemann zeta function:
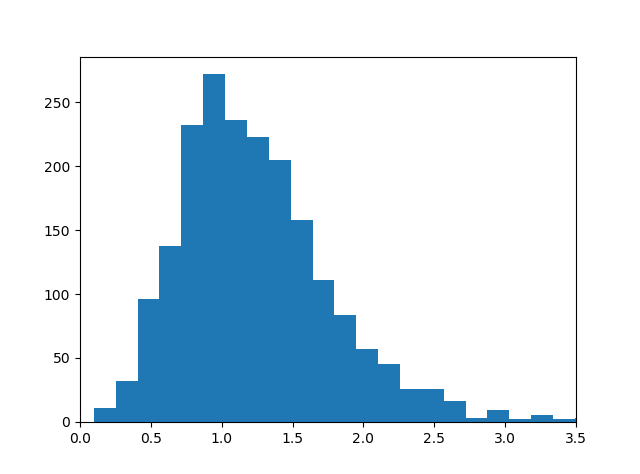
The distribution of random matrix eigenvalues is known exactly. I believe the distribution of the Riemann zeta function zeros is conjectural but persuasive. Here’s a plot using the first 100,000 zeros.
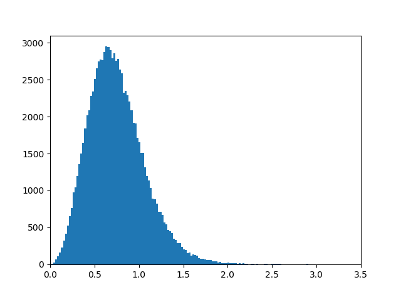

If I understand correctly the one of the crucial parts of the universality of eigenvalue distributions is that (in the limit of the rank n of the matrices going to infinity) they only depend on the symmetry of the matrices (arbitrary, Hermitian, symmetric, skew symmetric, …) but not on the distribution of the entries themselves as long as a few moments (typically fourth order) decay like that of the corresponding Gaussian ensemble.
See this survey of Terrence Tao and Van Vu
https://arxiv.org/pdf/1202.0068.pdf
and Tao’s blog.
https://terrytao.wordpress.com/2012/06/11/random-matrices-universality-of-local-spectral-statistics-of-non-hermitian-matrices/
https://terrytao.wordpress.com/2012/02/02/random-matrices-the-universality-phenomenon-for-wigner-ensembles/
https://terrytao.wordpress.com/2011/02/01/the-wigner-dyson-mehta-bulk-universality-conjecture-for-wigner-matrices/
https://terrytao.wordpress.com/2011/03/16/random-matrices-universality-of-eigenvectors/
and last not least this sweet set of slides
https://terrytao.files.wordpress.com/2011/01/universality.pdf
I watched the video and was very impressed by Wigner’s work. I really liked the book, “The Strangest Man”, by Graham Farmelo, about Dirac, can you recommend any biographies on Wigner?