The Fourier series of an odd function only has sine terms—all the cosine coefficients are zero—and so the Fourier series is a sine series.
What is the sine series for a sine function? If the frequency is an integer, then the sine series is just the function itself. For example, the sine series for sin(5x) is just sin(5x). But what if the frequency is not an integer?
For an odd function f on [-π, π] we have
where the coefficients are given by
So if λ is not an integer, the sine series coefficients for sin(λx) are given by
The series converges slowly since the coefficients are O(1/n).
For example, here are the first 15 coefficients for the sine series for sin(1.6x).
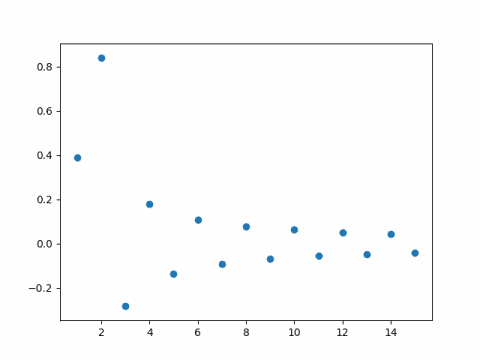
And here is the corresponding plot for sin(2.9x).
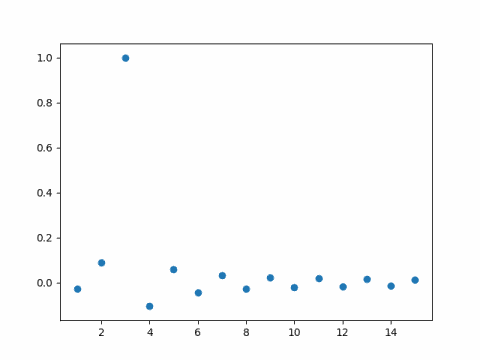
As you might expect, the coefficient of sin(3x) is nearly 1, because 2.9 is nearly 3. What you might not expect is that the remaining coefficients are fairly large.
Update: After writing this post I wrote another on the rate of convergence for Fourier series. In general, the smoother the function, the faster the Fourier series converges and vice versa, with some fine print.
The sine function above is perfectly smooth, but it’s Fourier series converges slowly. How can that be? The Fourier series is defined for periodic functions. If k is not an integer and we force sin(kx) to be a function with period 2π, it is not continuous. When we extend sin(kx) to make it periodic, there’s a jump discontinuity at the ends of each period.
Look back at
This equation can’t hold everywhere. If k is not an integer and f(x) = sin(kx), then the right size is zero at π but the left is not. In fact we’ll see Gibbs phenomenon at π because of the discontinuity there.
