{div, grad, curl} of a {div, grad, curl}

Posted on 3 December 2022 by John

The various combinations of divergence, gradient, and curl are confusing to someone seeing them for the first time, and even for someone having seen them many times. Is the divergence of a curl zero or is it the divergence of a gradient that’s zero? And there’s another one, Is it curl of curl or or curl of grad that’s zero?

It’s a mess that’s hard to sort out without pulling out differential forms. This post will show how a calculus student could make some sense out of all this, and how differential forms clarify the situation further.

Vector calculus perspective

We’ll start out looking at things from the perspective of a calculus student. We can make a table of all nine possible combinations of {grad, curl, div} applied to a {grad, curl, div} and start by asking which combinations make sense.

Gradient is something that takes a scalar function and returns a vector field. Curl takes a vector field and returns another vector field. Divergence takes a vector field and returns a scalar function. This means that only five of our nine combinations are even defined.

It turns out that the divergence of a curl is zero, and the curl of a gradient is zero (the zero vector). The other three possibilities are defined, but they are not zero in general.

So we can extend our chart to include the zeros.

Plain text version of chart image included at the bottom of the post.

Differential form perspective

From the perspective of differential forms, a scalar function f is a 0-form.

The differential of a 0-form is a 1-form and corresponds to the gradient.

The differential of a 1-form is a 2-form and corresponds to curl.

The differential of a 2-form is a 3-form and corresponds to divergence.

The differential of a differential is 0: d² = 0. This holds for k forms in general, for any non-negative integer k. So the curl of a gradient is 0 and the divergence of a curl is 0.

Gradients are 1-forms and curls are 2-forms. They’re different kinds of things. Vector calculus hides this distinction, which initially makes things simpler but ultimately makes things harder.

Now what about the three possibilities marked with question marks in the table above: the divergence of a gradient, the curl of a curl, and the gradient of a divergence?

From the perspective of differential forms, these are illegal operations. You cannot take the divergence of a gradient, because divergence operates on 2-forms, and a gradient is a 1-form. Similarly, you cannot take the curl of a curl or the gradient of a divergence. You could think of differential forms as adding type-checking to vector calculus.

But operations like taking the divergence of a gradient are legal in vector calculus. What gives?

Hodge star

The Hodge star operator is a duality between k-forms and (n–k)-forms. In vector calculus n = 3, and so the Hodge star takes 0-forms to 3-forms and 3-forms to 0-forms.

f ︎↔︎ f dx dy dz

It also takes 1-forms to 2-forms and 2-forms to 1-forms.

f dx + g dy + h dz ︎↔︎ f dy dz + g dz dx + h dx dy.

You can’t take the divergence of a gradient of a function f, but you can translate the 1-form df represents into the 2-form *df via the Hodge operator, then take the divergence of that. This gives you a 3-form d*df, which you can translate to a 0-form by applying * once more to get *d*df. So the Laplacian, defined to be the divergence of the gradient in vector calculus, is *d*d in the language of differential forms.

Curl takes 1-forms to 2-forms, so you can’t take the curl of a curl. But you can turn a curl into a 1-form via the Hodge operator and then take the curl of that. And while you can’t take the divergence of a gradient, you can take the divergence of the Hodge operator applied to a gradient.

In vector calculus the Hodge operator is invisible. Making it visible explains why some combinations of operators always result in zeros and some do not: some identities follow from the general identity d² = 0, but operations requiring a Hodge operator are not zero in general.

The Hodge star operator is not so simple in general as it is in Euclidean space. On a Riemann manifold the Hodge operator is defined in terms of the metric. Defining the Laplace operator as *d*df extends to Riemann manifolds, but defining it as the sum of second partial derivatives will not.

Plain text chart:

|------+------+------+-----|
|      | grad | curl | div |
|------+------+------+-----|
| grad | NA   | NA   | ?   |
| curl | 0    | ?    | NA  |
| div  | ?    | 0    | NA  |
|------+------+------+-----|

Nephroids and evolutes

Posted on 4 November 2022 by John

The previous post looked at the evolute of an ellipse. This post will look at evolutes more generally, and then look at nephroids.

As a quick reminder, given a curve c, a point on its evolute is the center of curvature for a point on c. See the previous post for a detailed example.

If a curve has a parameterization (x(t), y(t))^T then its evolute has parameterization

$\begin{pmatrix}x(t) \\ y(t) \end{pmatrix} - \frac{x'(t)^2+y'(t)^2}{x'(t) y''(t)-x''(t) -y'(t)} \begin{pmatrix}y'(t) \\ x'(t) \end{pmatrix}$

Nephroid curve

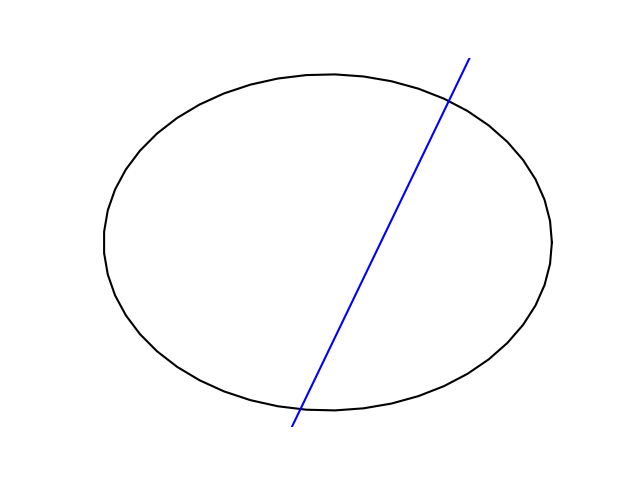
Let’s apply this to a nephroid. This word comes from the Greek for kidney-shaped. Comes from the same root as nephrology.

A nephroid can be parameterized by

$\begin{pmatrix} 3\cos t - \cos 3t \\ 3\sin t - \sin 3t \end{pmatrix}$

When we compute the evolute for this curve we get

$\begin{pmatrix} 2\cos^3 t \\ (2 + \cos 2t)\sin t \end{pmatrix}$

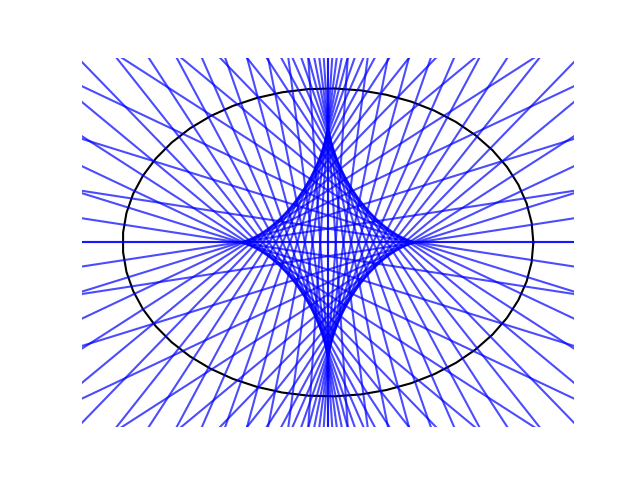
It’s not apparent from the expression above that the evolute of an nephroid is another nephroid, but it is clear from the plot below.

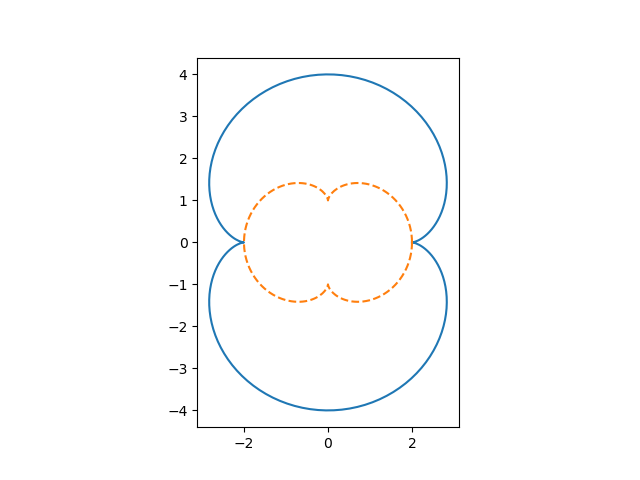
The solid blue curve is the nephroid, and the dashed orange curve is its evolute. Apparently the evolute is another nephroid, rotated and rescaled. We’ll come back to the equations shortly, but let’s look at another example first.

Cayley’s sextit

There is a curve known as Cayley’s sextit that has parameterization

$\begin{pmatrix} \cos^3 (t/3) \,\cos (t) \\ \cos^3 (t/3) \,\sin (t) \end{pmatrix}$

When we compute the evolute of this curve we get

$\begin{pmatrix} -\cos^2(t/3) (-2 \cos(2t/3) + \cos(4t/3)) / 2 \\ \sin^3(2t/3)/4 \end{pmatrix}$

When we plot Cayley’s sextit and its evolute we get

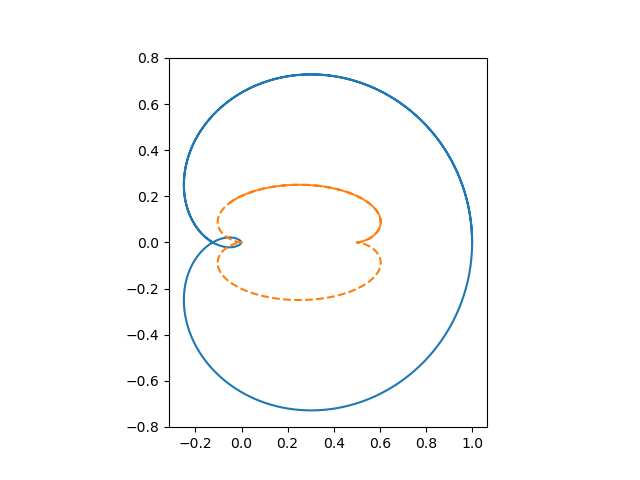
Note that to get the full curve of the evolute we let t run from 0 to 4π.

Again it’s not at all obvious from the equations, but apparently the evolute of Cayley’s sextit is also a nephroid, this time scaled, stretched, and shifted.

This says that pre-evolutes are not unique: two different curves can have the same (family) of evolutes.

Algebra

Now for the hard part: doing the algebra to show that the curves that look like nephroids are indeed nephroids.

We need to show that the set of points traced out by the evolute is a set of points on a nephroid: we don’t have to show that our parameterization of the evolute can be turned into our parameterization of a nephroid. So we shift to an implicit equation for a nephroid, scaled by a factor a:

$((x^2 + y^2 - 4a^2)^3 = 180 \,a^4 y^2$

Nephroid evolute

First let’s show that the evolute of a nephroid is a nephroid. From the plot it appears that the evolute is scaled by 1/2 and rotated a quarter turn. So we suspect that if we reverse x and y and multiply both by 1/2 we’ll get a nephroid. Let’s let Mathematica verify this for us:

    implicit[x_, y_, a_] := (x^2 + y^2 - 4 a^2)^3 - 108 a^4 y^2
    Simplify[implicit[(2 + Cos[2 t]) Sin[t], 2 Cos[t]^3, 1/2]]

Without calling Simplify we get something that isn’t obviously zero, but applying trig identities can reduce it to zero.

Cayley’s sextit evolute

In order to show that the evolute of Cayley’s sextit is a nephroid, we have to find what nephroid we believe it is.

Let’s look at the our parameterization of a nephroid again:

$\begin{pmatrix} 3\cos t - \cos 3t \\ 3\sin t - \sin 3t \end{pmatrix}$

We can see that the two cusps are at (-2, 0) and (2, 0), and the minimum and maximum heights are (0, -4) and (0, 4). We’ll line these points up with their counterparts in the evolute to Cayley’s sextit. Let’s look at its parameterization.

$\begin{pmatrix} -\cos^2(t/3) (-2 \cos(2t/3) + \cos(4t/3)) / 2 \\ \sin^3(2t/3)/4 \end{pmatrix}$

The two cusps correspond to y = 0, which happens when t = 0 and t = 3π/2. The corresponding x values are 1/2 and 0. This suggests the center of our nephroid is at 1/4 and our nephroid has been scaled by 1/8 in the horizontal direction.

The top and bottom correspond to x = 1/4, which happens when t = 3π/4 and t = 9π/4, and so our nephroid has height 1/4. This says our nephroid has been scaled by 1/16 in the vertical direction.

So if we shift x by 1/4 then multiply by 8, and multiply y by 16, we suspect we’ll get a standard nephroid. Let’s see what Mathematica has to say.

    implicit[8(-Cos[t/3]^2 (-2 Cos[2 t/3] + Cos[4 t/3])/2 - 1/4), 
        16 Sin[2 t/3]^3/4, 1]

This confirms that our guesses were correct. The evolute of Cayley’s sextit is indeed a nephroid, and we’ve identified which nephroid it is.

Evolute of an ellipse

Posted on 4 November 2022 by John

Suppose you’re standing on an ellipse. (You actually are: lines of longitude are elliptical because of earth’s equatorial bulge.)

Now draw a line perpendicular to where you’re standing. Lines of longitude are nearly circles, but we’ll look at a more obviously elliptical ellipse.

ellipse with one normal line

The line is perpendicular to the northeast side of the ellipse where it starts, but not where it crosses on the other side.

Now suppose lots of people standing on the circle all draw perpendicular lines. We get a surprising result.

If we did this with a circle, all we’d see is lines radiating out of the center of the circle. But for an ellipse we get something much more interesting.

There’s a simple equation for the star-like figure in the middle created by all the normal lines. We’ll get to that shortly, but first we need to talk about kissing circles.

Kissing circles

Suppose you wanted to approximate an ellipse by pieces of a circle, as is sometimes done in computer graphics. What radius should you use?

The circle that best approximates a curve at a point is called the kissing circle, or classically the osculating circle. The radius of this circle is the radius of curvature at the point where it touches the curve.

ellipse with two kissing circles

In the image above, the small blue circle is the best approximation of the ellipse on the side. The much bigger green circle is the best approximation to the ellipse on the top. The centers of these two circles are the centers of curvature at the two points on the curve.

Equation of evolute

We could visualize all centers of curvature by plotting the center of curvature for each point on the curve. This is called the evolute of the curve.

If we parameterize our ellipse by

x(t) = a cos t
y(t) = b sin t

then the evolute has parameterization

x(t) = (a² – b²) cos³ t / a
y(t) = (b² – a²) sin³ t / b

You can find a general formula for the evolute to any parameterized curve in the next post.

Here’s what it looks like.

This is the same shape as the figure formed by the normal lines at the top of the post. The lines that are normal to the ellipse are tangent to its evolute. To confirm this, we’ll plot the normal lines again and plot the evolute on top in red.

Incidentally, the evolute of an ellipse can extend outside the ellipse, and it will if the ellipse is more eccentric. Here’s an example.

The next post looks at a curve whose evolute is another curve of the same kind.

How to calculate length of an elliptic arc

Posted on 2 November 2022 by John

This post will show how to find the length of piece of an ellipse and explain what elliptic integrals have to do with ellipses.

Assume we have an ellipse centered at the origin with semi-major axis a and semi-minor axis b. So a > b > 0, the longest diameter of the ellipse is 2a and the shortest is 2b. The ellipse can be parameterized by

$\begin{align*} x(t) &= a \cos(t) \\ y(t) &= b \sin(t) \end{align*}$

Special case: quarter of an ellipse

Let’s first find the perimeter of a 1/4 of the ellipse.

one quarter of an ellipse highlighted in red

This is given by the integral

$\int_0^{\pi/2} \sqrt{a^2 \sin^2(t) + b^2 \cos^2(t)}\, dt$

The change of variables u = π/2 – t turns the integral into

$\begin{align*} \int_0^{\pi/2} \sqrt{a^2 \cos^2(u) + b^2 \sin^2(u)}\, du &= a \int_0^{\pi/2} \sqrt{1 - \left(1 - b^2/a^2 \right) \sin^2(u)}\, du \\ &= a E\left(1 - b^2/a^2 \right) \end{align}$

because E, the “elliptic integral of the second kind,” is defined by

$E(m) = \int_0^{\pi/2} \sqrt{1 - m\sin^2 t}\, dt$

Therefore the perimeter of the entire ellipse is 4E(1 – b²a²). Let’s define

for the rest of the post. Incidentally, m = e² where e is the eccentricity of the ellipse.

General case

Now let’s find the length of an arc where t ranges from 0 to T and T is not necessarily π/2.

general elliptic segment highlighted in red

The derivation is similar to that above.

$\begin{align*} \int_0^T \sqrt{a^2\sin^2(t) + b^2\cos^2(t)}\, dt &= \int_{\pi/2 - T}^{\pi/2} \sqrt{a^2\cos^2u + b^2\sin^2u} \, du \\ &= a E(m) - a \int_0^{\pi/2 - T} \sqrt{1 - m \sin^2u} \, du \\ &= aE(m) -aE(\pi/2 - T, m) \\ &= a E(m) + a E(T - \pi/2, m) \end{align*}$

where E, now with two arguments, is the “incomplete elliptic integral of the second kind” defined by

$E(\varphi, m) = \int_0^\varphi \sqrt{1 - m\sin^2(t)} \,dt$

It is “incomplete” because we haven’t completed the integral by integrating all the way up to π/2.

To find the length of a general arc whose parameterization runs from t = T₀ to t = T₁ we find the length from 0 out to T₁ and subtract the length from 0 out to T₀ which gives us

$a E(T_1 - \pi/2, m) - a E(T_0 - \pi/2, m)$

The elliptic integrals are so named because they came out of the problem we’re looking at in this post. The integrals cannot be computed in elementary terms, so we introduce new functions that are defined by the integrals. I expand this idea in this post.

NB: We are specifying arcs by the range of our parameterization parameter t, not by the angle from the center of the ellipse. If our ellipse were a circle the two notions would be the same, but in general they are not. The central angle θ and the parameter T are related via

$\begin{align*} \theta &= \arctan\left( \frac{b}{a} \tan T \right) \\ T &= \arctan\left( \frac{a}{b} \tan\theta \right) \end{align*}$

I wrote about this here.

Python code

Let’s calculate the length of an arc two ways: using our formula and using numerical integration. Note that the Python implementation of the (complete) elliptic integral is ellipe and the implementation of the incomplete elliptic integral is ellipeinc. The “e” at the end of ellipe distinguishes this elliptic integral, commonly denoted by E, from other kinds of elliptic integrals.

    
    from numpy import pi, sin, cos
    from scipy.special import ellipe, ellipeinc
    from scipy.integrate import quad
    
    def arclength(T0, T1, a, b):
        m = 1 - (b/a)**2
        t1 = ellipeinc(T1 - 0.5*pi, m)
        t0 = ellipeinc(T0 - 0.5*pi, m)
        return a*(t1 - t0)
    
    def numerical_length(T0, T1, a, b):
        f = lambda t: (a**2*sin(t)**2 + b**2*cos(t)**2)**0.5
        return quad(f, T0, T1)
        
    T0, T1, a, b = 0, 1, 3, 2
    y, err = numerical_length(T0, T1, a, b)
    ell = arclength(T0, T1, a, b)
    assert(abs(ell - y) < 1e-12)

    T0, T1, a, b = 7, 1, 4, 3
    y, err = numerical_length(T0, T1, a, b)
    ell = arclength(T0, T1, a, b)
    assert(abs(ell - y) < 1e-12)

The tests pass. This increases our confidence that the derivation above is correct.

Trig in hyperbolic geometry

Posted on 8 September 2022 by John

I recently wrote posts about spherical analogs of the Pythagorean theorem, the law of cosines, and the law of sines. The corresponding formulas for hyperbolic space mostly just replace circular functions with hyperbolic functions, i.e. replace sine with hyperbolic sine and cosine with hyperbolic cosine.

Triangles on a sphere or on a hyperbolic space like a pseudosphere have two kinds of angles: the sides come together at an angle, but the sides themselves are angles. By convention, the former are denoted with upper case letters and the latter with lower case letters.

The translation rule from spherical to hyperbolic geometry is to change functions of sides from circular to hyperbolic, but to leave functions of intersection angles alone. Or in typographical terms, put an h on the end of functions of a lower case letter but not functions of a upper case letter.

You can find these formulas, for example, in [1].

Hyperbolic Pythagorean theorem

The Pythagorean theorem on a sphere

cos(c) = cos(a) cos(b).

becomes

cosh(c) = cosh(a) cosh(b)

in hyperbolic geometry. Here you simply change cos to cosh.

Hyperbolic law of sines

The law of sines on a sphere

sin(a) / sin(A) = sin(b) / sin(B) = sin(c) / sin(C).

becomes

sinh(a) / sin(A) = sinh(b) / sin(B) = sinh(c) / sin(C).

in hyperbolic geometry. Here sin becomes sinh, but only before a lower case letter, i.e. when applied to a side.

Hyperbolic law of cosines

The law of cosines on a sphere

cos(c) = cos(a) cos(b) + sin(a) sin(b) cos(C).

becomes

cosh(c) = cosh(a) cosh(b) – sinh(a) sinh(b) cos(C).

Note the negative sign, a small exception to our conversion rule.

We could rewrite the law of cosines on a sphere to be

cos(c) = cos(a) cos(b) + κ sin(a) sin(b) cos(C)

where κ stands for curvature, which equals 1 for a unit sphere. Then our theorem translation rule holds exactly:

cosh(c) = cosh(a) cosh(b) + κ sinh(a) sinh(b) cos(C)

in a hyperbolic space with curvature κ = -1.

See this post on the Unified Pythagorean Theorem for a version of the Pythagorean theorem that holds in spherical, plane, and hyperbolic geometry.

Maybe there are analogous unified laws of sines and cosines. This is left as an exercise for the reader.

[1] William P. Thurston. Three-Dimensional Geometry and Topology, Volume 1. Princeton University Press, 1997.

Radius, circumference, and area in non-Euclidean geometry

Posted on 28 August 2022 by John

How does the circumference of a circle vary with its radius? What about the area? The answers are simple and familiar in Euclidean geometry, but not as simple or as familiar in non-Euclidean geometry.

This post will look at how circumference and area vary as a function of radius in three spaces: a surface with constant curvature 1 (i.e. a unit sphere), a surface of constant curvature 0 (i.e. a plane), and a surface of constant curvature -1 (a hyperbolic surface). The radius in each case is the distance from the center to the circle as measured on the surface.

Spherical case

In the spherical case, a circle of radius r has circumference

C(r) = 2π sin(r)

and area

A(r) = 2π (1 – cos(r)).

The circumference formula is valid for 0 ≤ r ≤ π and the area formula is valid for 0 ≤ r ≤ π/2.

Hyperbolic case

In the hyperbolic case, a circle of radius r has circumference

C(r) = 2π sinh(r)

and area

A(r) = 2π (cosh(r) – 1).

These formulas are valid for 0 ≤ r < ∞.

Plots

Let’s make a couple plots to illustrate the equations above. First, circumference as a function of radius.

The top subplot looks surprising at first. Can circumference decrease when radius increases? Yes, on a sphere. Imagine a circle around the north pole. As we pull that circle down from the pole, the circumference increases until the circle becomes the equator. Past that point, the circumference of the circle decreases as the circle descends further south.

Using the same range of r for all three subplots obscures the fact that the circumference of a circle in the hyperbolic case grows exponentially with the radius.

Next let’s look at area as a function of radius.

In each case, area grows approximately quadratically with radius. But again the growth in the hyperbolic case is exponential as r increases further than is possible in the spherical case.

One last note: In the plane, the ratio of area to circumference is proportional to r. In the hyperbolic case, the same ratio is asymptotically constant, independent of r.

Update

Here’s a plot of C(r) / r.

And here’s a plot of A(r) / r².

Unified Pythagorean Theorem

Posted on 27 August 2022 by John

A few days ago I wrote that the spherical counterpart of the Pythagorean theorem is

cos(c) = cos(a) cos(b)

where sides a and b are measured in radians. If we’re on a sphere of radius R and we measure the sides in terms of arc length rather than in radians, the formula becomes

cos(c/R) = cos(a/R) cos(b/R)

because an of length x has angular measure x/R.

How does this relate to the more familiar Pythagorean theorem on the plane? If a, b, and c are small relative to R, then the plane Pythagorean theorem holds approximately:

c² ≈ a² + b².

Unified Pythagorean Theorem

In this post I’ll present a version of the Pythagorean theorem that holds exactly on the sphere and the plane, and on a pseudosphere (hyperbolic space) as well. This is the Unified Pythagorean Theorem [1].

A sphere of radius R has curvature 1/R². A plane has curvature 0. A hyperbolic plane can have curvature k for any negative value of k.

Let A(r) be the area of a circle of radius r as measured on a surface of curvature k. Here area and radius are measured intrinsic to the surface. Then the Unified Pythagorean Theorem says

A(c) = A(a) + A(b) – k A(a) A(b) / 2π.

Plane

If k = 0, the final term on the right drops out, and we’re left with the ordinary Pythagorean theorem with both sides of the equation multiplied by π.

Sphere

On a sphere of radius R, the area of a circle of radius r is

A(r) = 2πR²(1 – cos(r/R)).

Note that for small x,

1 – cos(x) ≈ x²/2,

and so A(r) ≈ πr² when R ≫ r. (Notation explained here.)

When you substitute the above definition for A in the unified theorem and plug in k = 1/R² you get

cos(c/R) = cos(a/R) cos(b/R)

as before.

Pseudosphere

In a hyperbolic space of curvature k < 0, let R = 1/√(-k). Then the area of a circle of radius r is

A(r) = 2πR²(cosh(r/R) – 1)

As with the spherical case, this is approximately the plane area when R ≫ r because

cosh(x) – 1 ≈ x²/2

for small x. Substituting the definition of A for hyperbolic space into the Universal Pythagorean Theorem reduces to

cosh(c/R) = cosh(a/R) cosh(b/R),

which is the hyperbolic analog of the Pythagorean theorem. Note that this is the spherical Pythagorean theorem with cosines replaced with hyperbolic cosines.

[1] Michael P. Hitchman. Geometry with an Introduction to Cosmic Topology. Theorem 7.4.7. Available here.

Approximating a golden spiral with circular arcs

Posted on 10 May 2022 by John

The previous post included this image of a logarithm spiral passing through the corners of squares in a sequence of golden rectangles.

The portion of the spiral in each square looks like a quarter of a circle. How well would circular arcs approximate the spiral?

Very well. Here’s a plot.

The circular arc inside the blue square is plotted in blue, the arc inside the green box in green, etc. The logarithmic spiral is plotted on top with a dashed black line. You have to zoom in closely to see any difference between the logarithmic spiral and its circular approximations.

For aesthetic applications, circular arcs are good enough and probably easier to work with. For a sort of three-dimensional analog of this approximation, see this post on the geometry of the Sydney Opera House.

Sometimes discontinuities in first or second derivatives are visually noticeable, but here they’re not. The approximation of the logarithmic spiral by a sequence of quarter circles has a jumps in curvature, which is roughly a second derivative. I suppose it’s more noticeable when curvature jumps from positive to zero or from positive to negative. Here it’s jumping from one positive value (the reciprocal of the circle radius) to another positive value (the reciprocal of a smaller radius).

Area of spherical triangle

Posted on 29 November 2021 by John

A few days ago I wrote about how you could calculate the area of a spherical triangle by measuring the angles at its vertices. As was pointed out in the comments, there’s a much more direct way to find the area.

Folke Eriksson gives the following formula for area in [1]. If a, b, and c are three unit vectors, the spherical triangle formed by their vertices has area E where

$\tan\left(\frac{E}{2}\right) = \frac{|\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})|}{1 + \mathbf{a}\cdot \mathbf{b} + \mathbf{b}\cdot \mathbf{c} + \mathbf{a}\cdot \mathbf{c}}$

Let’s try the formula out with an example and compare the area to that of a flat triangle. We’ll pick three cities as our three points, assuming the earth is a unit sphere.

Let a = Austin, Texas, b = Boston, Massachusetts, and c = Calgary, Alberta. The spherical coordinates of each point will be (1, θ, φ) where θ is longitude and φ is π/2 minus latitude.

    from numpy import *
    
    def latlong_to_cartesian(latlong):
        phi   = deg2rad( 90 - latlong[0] )
        theta = deg2rad( latlong[1] )
    
        x = sin(phi) * cos(theta)
        y = sin(phi) * sin(thea)
        z = cos(phi)
        return array([x,y,z])
    
    def spherical_area(a, b, c):
        t = abs( inner(a, cross(b, c) ) )
        t /= 1 + inner(a,b) + inner(b,c) + inner(a,c)
        return 2*arctan(t)
    
    def flat_area(a, b, c):
        x = cross(a - b, c - b)
        return 0.5*linalg.norm(x)
    
    # Latitude and longitude
    austin  = (30.2672,  97.7431)
    boston  = (42.3584,  71.0598)
    calgary = (51.0501, 114.0853)
    
    a = latlong_to_cartesian(austin)
    b = latlong_to_cartesian(boston)
    c = latlong_to_cartesian(calgary)
    
    round = spherical_area(a, b, c)
    flat  = flat_area(a, b, c)
    print(round, flat, round/flat)

This shows that our spherical triangle has area 0.0900 and the corresponding Euclidean triangle slicing through the earth would have area 0.0862, the former being 4.467% bigger.

Let’s repeat our exercise with a smaller triangle. We’ll replace Boston and Calgary with Texas cities Boerne and Carrollton.

    boerne  = (29.7947, 98.7320)
    carrollton = (32.9746, 96.8899)

Now we get area 0.000302 in both cases. The triangle is so small relative to the size of the earth that the effect of the earth’s curvature is negligible.

In fact the ratio of the two computed areas is 0.9999, i.e. the spherical triangle has slightly less area. The triangle is so flat that numerical error has a bigger effect than the curvature of the earth.

How could we change our code to get more accurate results for small triangles? That would be an interesting problem. Maybe I’ll look into that in another post.

[1] “On the measure of solid angles”, F. Eriksson, Math. Mag. 63 (1990) 184–187.

Triangles on a pseudosphere

Posted on 28 November 2021 by John

The previous post was about triangles on a sphere. This post will be about triangles on a pseudosphere.

A pseudosphere looks something like the bell of a trumpet or a trombone.

Here’s a plot of a pseudosphere.

This was created in Mathematica with the code

    ParametricPlot3D[
        {   
            Cos[p] Sech[t],
           -Sin[p] Sech[t],
            t - Tanh[t] 
        },
        {t,  0, 4},
        {p, 0, 2 Pi}
    ]

The pseudosphere has constant negative curvature just as the sphere has constant positive curvature.

By curvature I mean specifically Gaussian curvature, the product of the sectional curvature in orthogonal directions at each point. A sphere curves the same way in all directions. A pseudosphere curves opposite ways in different directions. Coordinate lines through a point are convex in one direction and concave in another. Their sectional curvatures have opposite signs and so their product is negative.

A spherical triangle is formed by great circles connecting the vertices of the triangles. Great circles are the geodesics on a sphere.

A pseudospherical triangle is a triangle formed by geodesics on the pseudosphere. These are the “straight” lines in the hyperbolic geometry of the surface.

On a sphere, the interior angles of a triangle add up to more than π, and in fact the amount by which the sum of the angles exceeds π is proportional to the area of the triangle.

On a pseudosphere, the interior angles of a triangle add up to less than π. And just as in the case of the sphere, the difference between the sum of the angles and π, now negative, is proportional to the area. This result was discovered by Johann Heinrich Lambert (1728–1777).

On a sphere or a pseudosphere, the interior angles of a small triangle add up to nearly π. As triangles get larger, the sum increases on a sphere but decreases on a pseudosphere.

The general principle behind both of these cases is the local Gauss-Bonnet theorem. For any surface, let T be triangle whose sides are geodesics. Then the integral of the Gaussian curvature over T is equal to the sum of the interior angles of T minus π.

When a surface has constant curvature, the integral of curvature over a region is proportional to the area of the region. So on a sphere or pseudosphere, the area of a geodesic triangle is proportional to the sum of the interior angles minus π.

The local Gauss-Bonnet theorem holds when the sides of a triangle are not geodesics, but in that case the theorem has an extra term, the integral of the geodesic curvature along the sides. Since the geodesic curvature of a geodesic is zero, this term drops out for geodesic triangles.

Vector calculus perspective

Differential form perspective

Hodge star

Related posts

Nephroid curve

Cayley’s sextit

Algebra

Nephroid evolute

Cayley’s sextit evolute

Kissing circles

Equation of evolute

Similar posts

Special case: quarter of an ellipse

General case

Python code

Hyperbolic Pythagorean theorem

Hyperbolic law of sines

Hyperbolic law of cosines

Related post

Spherical case

Hyperbolic case

Plots

Update

Related posts

Unified Pythagorean Theorem

Plane

Sphere

Pseudosphere

Related posts

Related posts