A few days ago I wrote about how to estimate 10x. This is an analogous post for
exp(x) = ex.
We will assume -0.5 ≤ x ≤ 0.5. You can bootstrap your way from there to other values of x. For example,
exp(1.3) = exp(1 + 0.3) = e exp(0.3)
and
exp(0.8) = exp(1 – 0.2) = e / exp(0.2).
I showed here that
loge(x)≈ (2x – 2)/(x + 1)
for x between exp(-0.5) and exp(0.5).
Inverting both sides of the approximation shows
exp(x) ≈ (2 + x)/(2 – x)
for x between -0.5 and 0.5.
The maximum relative error in this approximation is less than 1.1% and occurs at x = 0.5. For x closer to the middle of the interval [-0.5, 0.5] the relative error is much smaller.
Here’s a plot of the relative error.
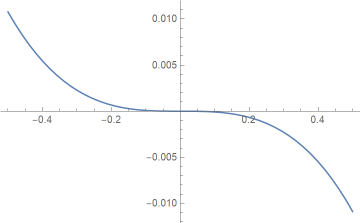
This was produced with the following Mathematica code.
re[x_] := (Exp[x] - (2 + x)/(2 - x))/Exp[x]
Plot[re[x], {x, -0.5, 0.5}]
Update: The approximations from this post and several similar posts are all consolidated here.

Typo in log_e formula: 2nd – must be a +
(and (x) argument is missing).
Thanks!